
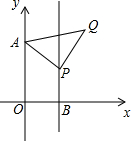
 如图,已知在平面直角坐标系xOy中,O为坐标原点,A(0,5),B(3,0),过点B作直线l∥y轴,点P(3,b)是直线l上的一个动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P在直线l上运动时,点Q也随时之运动,问:当b=$\frac{23}{7}$时,AQ+BQ的值最小为$\sqrt{130}$.
如图,已知在平面直角坐标系xOy中,O为坐标原点,A(0,5),B(3,0),过点B作直线l∥y轴,点P(3,b)是直线l上的一个动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P在直线l上运动时,点Q也随时之运动,问:当b=$\frac{23}{7}$时,AQ+BQ的值最小为$\sqrt{130}$. 分析 如图作PM⊥OA于M,QN⊥MP于N,首先证明点Q在直线y=-x+11上运动,然后利用对称找到点AQ+BQ最小时的位置,即可解决问题.
解答 解:如图作PM⊥OA于M,QN⊥MP于N,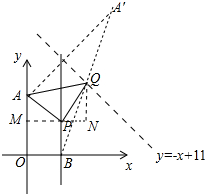 ∵PA=PQ,∠APQ=90°,
∵PA=PQ,∠APQ=90°,
∵∠APM+∠QPN=90°,∠QPN+∠PQN=90°,
∴∠APM=∠PQN,
在△PAM和△QPN中,
$\left\{\begin{array}{l}{∠AMP=∠PNQ}\\{∠APM=∠PQN}\\{AP=PQ}\end{array}\right.$,
∴△PAM≌△QPN,
∴QN=PM=3,AM=PN=5-b,
∴点Q坐标为(8-b,3+b),
∵8-b+3+b=11,
∴点Q在直线x+y=11,即y=-x+11上,
∵点A关于直线y=-x+11是对称点A′(6,11),连接BA′与直线y=-x+11的交点为Q,此时QA+QB最小,
这个最小值=A′B=$\sqrt{(6-3)^{2}+1{1}^{2}}$=$\sqrt{130}$.
∵直线BA′为y=$\frac{11}{3}$x-11,
由$\left\{\begin{array}{l}{y=-x+11}\\{y=\frac{11}{3}x-11}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{33}{7}}\\{y=\frac{44}{7}}\end{array}\right.$,
∴8-b=$\frac{33}{7}$,
∴b=$\frac{23}{7}$.
故答案分别为$\frac{23}{7}$,$\sqrt{130}$.
点评 本题考查轴对称、线段最短问题,题目比较难,本题的突破点是证明点Q在直线y=-x+11上,学会转化的思想,把不会的题目转化为我们熟悉的题目,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2)且tan∠ABC=$\frac{1}{2}$;
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2)且tan∠ABC=$\frac{1}{2}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -x2+2 | B. | x3+4 | C. | x3-4x+4 | D. | x3-2x2-2x+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y1=ax2+bx过(-2,4),(-4,4)两点.
如图,已知二次函数y1=ax2+bx过(-2,4),(-4,4)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com