
如图所示,P为△ABC中BC边的垂直平分线上的一点,且∠PBG=![]() ∠A,BP、CP分别交AC、AB于点D、E.求证:BE=CD.
∠A,BP、CP分别交AC、AB于点D、E.求证:BE=CD.

|
证明:作 BM⊥CE于M,CN⊥BD于N,∴∠ BMP=∠CNP=∵ PG为BC的垂直平分线,∴ PB=PC∴△ MPB=∠NPC,∴△ MPB≌△NPC(AAS),∴ BM=CN.(本题要求证明的两条线段的相等关系一般利用三角形全等可以得出结论.)∴ PB=PC,∴∠ PBG=∠PCG,∴∠ MPB=∠PBG+∠PCG= 2∠PBG.∵∠ PBG=∴∠ MPB=∠A,∴∠ MEB=∠MPB+∠PBE=∠ A+∠PBE=∠ NDC.∵ BM=CN,∠ BME=∠CND=∠ MEB=∠NDC,∴△ MEB≌△NDC(AAS),∴ BE=CD. |
|
注:本题在证明三角形全等时可以发现,结论中的两条线段所在的三角形△ BEP和△CDP不可能全等,所以需添加辅助线构造新的全等三角形.通过运用垂直平分线的性质,并结合已知角的关系,给题目的证明提供了条件. |


科目:初中数学 来源:《19.6 相似三角形的性质》2010年同步练习(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:《24.3 相似三角形的性质》2009年同步练习(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源: 题型:
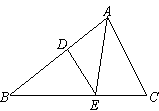
如图所示,D为AB边上一点,AD∶DB=3∶4,DE∥AC交BC于点E,则S△BDE∶S△AEC等于( )
A.16∶21 B.3∶7 C.4∶7 D.4∶3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com