
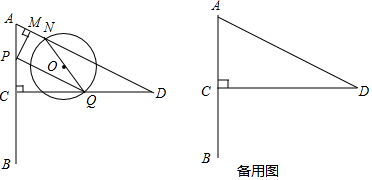
分析 (1)在Rt△ACD中,利用勾股定理即可求出AD,根据cosA=$\frac{AM}{AP}$=$\frac{AC}{AD}$,构建方程即可求出AM.
(2)由tan∠D=tan∠PQC,推出∠D=∠PQC,推出PQ∥AD即可解决问题.
(3)①分两种情形当P在线段AC上,即0<x≤4时.当P在线段BC上,即4<x<8时,分别构建方程即可解决问题.
②分两种情形当P在AC上,当P在线段BC上,分别构建方程即可解决问题.
解答 解:(1)在Rt△ACD中,AC=BC=$\frac{1}{2}$AB=4,CD=AB=8,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$.
∵cosA=$\frac{AM}{AP}$=$\frac{AC}{AD}$,
∴$\frac{AM}{x}$=$\frac{4}{4\sqrt{5}}$,
∴AM=$\frac{\sqrt{5}}{5}$x.
故答案为4$\sqrt{5}$,$\frac{\sqrt{5}}{5}$x;
(2)如图1中,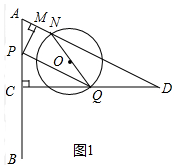
∵tan∠D=$\frac{AC}{CD}$=$\frac{1}{2}$,tan∠PQC=$\frac{PC}{CQ}$=$\frac{1}{2}$,
∴tan∠D=tan∠PQC,
∴∠D=∠PQC,
∴PQ∥AD,
∵PM⊥AD,
∴PM⊥PQ,
∴∠MPQ=90°;
(3)①当P在线段AC上,即0<x≤4时,
∵⊙O与BC相切,
∴NQ⊥CD,
∵AP=x,
∴CP=4-x,CQ=2PC=8-2x,DQ=8-(8-2x)=2x,DN=AD-2AM=4$\sqrt{5}$-$\frac{2\sqrt{5}}{5}$x,
∵cos∠D=$\frac{CD}{AD}$=$\frac{DQ}{DN}$,
∴$\frac{2x}{4\sqrt{5}-\frac{2\sqrt{5}}{5}x}$=$\frac{8}{4\sqrt{5}}$,
∴x=$\frac{20}{7}$.
当P在线段BC上,即4<x<8时,同理可得$\frac{CD}{AD}$=$\frac{DQ}{DN}$,
∵CP=AP-AC=x-4,CQ=2CP=2x-8,DQ=CD-CQ=16-2x,
∴$\frac{16-2x}{4\sqrt{5}-\frac{2\sqrt{5}}{5}x}$=$\frac{8}{4\sqrt{5}}$,
∴x=$\frac{20}{3}$.
综上所述,x=$\frac{20}{7}$或$\frac{20}{3}$时,⊙O与CD相切.
②当P在AC上时,由题意PN=AP=x,
易证△PQI≌△PQC,可得PI=PC=4-x,
∵IN=1,
∴PI+IN=PN,
∴4-x+1=x,
∴x=$\frac{5}{2}$.
当P在线段BC上,设PN与CD的交点为点E,作NF⊥AB于F,
易知FN=$\frac{4}{5}$x,PF=$\frac{3}{5}$x,则CE=$\frac{4(x-4)}{3}$,PE=$\frac{5(x-4)}{3}$,
∴EN=x-$\frac{5(x-4)}{3}$=$\frac{20-2x}{3}$,EQ=(2x-8)-$\frac{4(x-4)}{3}$=$\frac{2x-8}{3}$,
EI=EN-IN=$\frac{17-2x}{3}$,
在Rt△EQI中,cos∠IEQ=$\frac{EI}{EQ}$=$\frac{4}{5}$,
∴$\frac{17-2x}{3}$=$\frac{4}{5}$×$\frac{2x-8}{3}$,
∴x=$\frac{13}{2}$.
点评 本题考查圆综合题、切线的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用构建方程的思想思考问题,学会分类讨论不能漏解,属于中考压轴题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:解答题
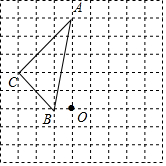 如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.
如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
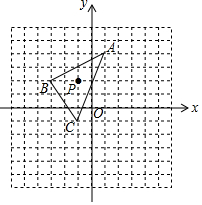 如图,△ABC中任意一点P(m,n),经过平移后对应点P1(m+4,n-3),将△ABC作同样的平移得到△A1B1C1,已知A(1,4)、B(-3,2),C(-1,-1).
如图,△ABC中任意一点P(m,n),经过平移后对应点P1(m+4,n-3),将△ABC作同样的平移得到△A1B1C1,已知A(1,4)、B(-3,2),C(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
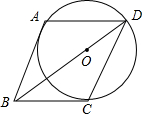 如图,菱形ABCD的顶点A,D,C均在⊙O上,且BC边与⊙O相切于点C.
如图,菱形ABCD的顶点A,D,C均在⊙O上,且BC边与⊙O相切于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com