
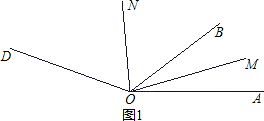
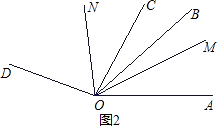
 ∠AOB,∠BON=
∠AOB,∠BON= ∠BOD
∠BOD ∠AOB+
∠AOB+ ∠BOD=
∠BOD= (∠AOB+∠BOD)
(∠AOB+∠BOD) ∠AOD=80°;
∠AOD=80°; ∠AOC,∠BON=
∠AOC,∠BON= ∠BOD
∠BOD ∠AOC+
∠AOC+ ∠BOD-∠BOC
∠BOD-∠BOC (∠AOC+∠BOD)-∠BOC
(∠AOC+∠BOD)-∠BOC ×180-20=70°;
×180-20=70°; ,
, ,
, ∠AOB,∠BON=
∠AOB,∠BON= ∠BOD.然后根据关系转化求出角的度数;
∠BOD.然后根据关系转化求出角的度数; ∠AOC+
∠AOC+ ∠BOD-∠BOC=
∠BOD-∠BOC= (∠AOC+∠BOD)-∠BOC;
(∠AOC+∠BOD)-∠BOC; ,
, ,由此列出方程求解即可.
,由此列出方程求解即可.

科目:初中数学 来源: 题型:
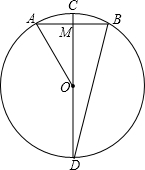 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;
如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;
如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com