
任画一个等边三角形,分别作出该三角形绕其某一顶点逆时针旋转60°,120°,180°,240°,300°后的图形,观察所作的图形,可知得到了一个 形.
科目:初中数学 来源: 题型:
 边形DEFG即为所求.
边形DEFG即为所求.查看答案和解析>>
科目:初中数学 来源: 题型:
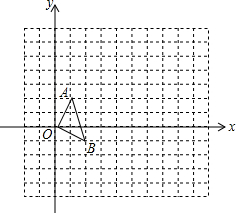 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).| 4 | 3 |

查看答案和解析>>
科目:初中数学 来源:2012年辽宁省建平县八年级单科数学竞赛卷(解析版) 题型:解答题
任画一个直角三角形,分别以它的三条边为边向外做等边三角形,
要求:(1)画出图形;
(2)探究这三个等边三角形面积之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建省福安市九年级中考模拟考试数学试卷(解析版) 题型:解答题
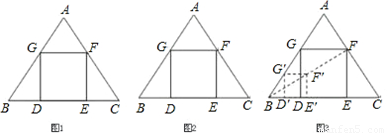
△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
(1) 证明:△BDG≌△CEF;
(2) 设△ABC的边长为2,请你帮小聪求出正方形的边长.(结果精确到十分位)
(3) 小颖想:不求正方形的边长我也能画出正方形.具体作法是:如图3
①在AB边上任取一点G′,如图作正方形G′D′E′F′;
②连接BF′并延长交AC于F;
③作FE∥F′E′交BC于E,FG∥F′G′交AB于G,GD∥G′D′交BC于D,则四边形DEFG即为所求.你认为小颖的作法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com