练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，梯形ABCD内接于⊙O，AD//BC，E是DA延长线上一点，AB2=AE·BC，BE和CA的延长线交于点F。
    （1）求证：BE是⊙O的切线；
    （2）已知BC=18，CD=12，AF=16，求BE和AD的长。
    解：（1）证明：∵AD//BC，∠ABC=∠EAB，
    ∵AB2=AE·BE，
    ∴，
    ∴△ABC∽△EAB，
    ∴∠1=∠2，
    连结OA，OB，
    ∵OA=OB，
    ∴∠3=∠BAO，
    ∴∠O+2∠3=180°，
    又∵∠O=2∠2，
    ∴2∠2+2∠3=180°，
    ∴∠1+∠3=90°，
    ∴∠EBO=90°，
    ∴OB⊥BF，又B点在⊙O上，
    ∴BF是⊙O的切线；
    （2）∵AD//BC，AB=CD，
    ∴AB=CD=12，
    ∵AB2=AE·BC，
    ∴，
    ∵AD//BC，
    ∴△EFA∽△FBC，
    ∴，
    ∴，
    ∴AC=20，
    由（1）知△ABC∽△EAB，
    ∴，
    ∴，
    由△EBA∽△EBD（或由切割线定理）得EB2=EA·ED，
    ∴，
    ∴AD=ED-EA=，
    综上，EB=，AD=为所求。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、如图，梯形ABCD内接于⊙O，BC∥AD，AC与BD相交于点E，在不添加任何辅助线的情况下：
    （1）图中共有几对全等三角形，请把它们一一写出来，并选择其中一对全等三角形进行证明；
    （2）若BD平分∠ADC，请找出图中与△ABE相似的所有三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E，若AD=5，AB=6，BC=9．
    （1）求DC的长；
    （2）求证：四边形ABCE是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，梯形ABCD内接于⊙O，AB∥CD，AB为直径，DO平分∠ADC，则∠DAO的度数是（　　）
    A、90°B、80°C、70°D、60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，梯形ABCD内接于⊙O，AD∥BC，E是DA延长线上一点，AB2=AE•BC，BE和CA的延长线交于点精英家教网F．
    （1）求证：BE是⊙O的切线；
    （2）已知BC=18，CD=12，AF=16，求BE和AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

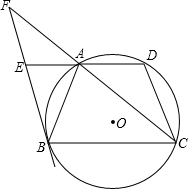    精英家教网如图，梯形ABCD内接于⊙O，AD∥BC，∠DAB=49°，则∠AOC的度数为
     
    ．

    查看答案和解析>>

    同步练习册答案