
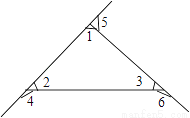
如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )
A. ①②③ B. ①②③④ C. ①②③④⑤ D. ①②④⑤
D 【解析】如图, ①∠1和∠4是直线AC和直线BC被直线AB截得的同位角,所以①正确; ②∠3和∠5是直线BC和直线AB被直线AC截得的内错角,所以②正确; ③∠2和∠6是直线AB和直线AC被直线CB截得的内错角,所以③错误; ④∠5和∠2是直线AC和直线BC被直线AB截得的同位角,所以④正确; ⑤∠1和∠3是直线BC和直线AB被直线AC截得的同旁内角,所以⑤... 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
在 中,
中,  ,
,  ,
,  ,则
,则 的余弦值等于( ).
的余弦值等于( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:单选题
为确保信息安全,信息需要加密传输,发送方由明文→密文(解密).接收方由密文→明文(解密)。已知加密规则为:明文a,b,c对应的密文a+1,2b+4,3c+9,例如明文1,2,3对应的密文2,8,18。如果接收方收到密文7,18,15,则解密得到的明文为( )
A. 4,5,6 B. 6,7,2 C. 2,6,7 D. 7,2,6
B 【解析】试题分析:首先根据必须理解密文的加密方法,然后进行计算.根据题意得:a+1=7,2b+4=18,3c+9=15 则a=6,b=7,c=2,即明文为6,7,2.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:填空题
如图,AB//CD,∠CDE=119º,GF交∠DEB的平分线EF于F,∠AGF=130º,则∠F= 。
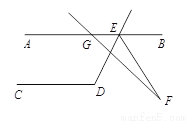
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:单选题
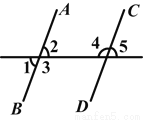
如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】②,④正确.②中∠5=70°,又∠2=∠1=70°(对顶角相等),所以∠5=∠2,所以AB∥CD(同位角相等,两直线平行);④中∠4=110°,又∠2=∠1=70°(对顶角相等),所以∠2+∠4=70°+110°=180°,所以AB∥CD(同旁内角互补,两直线平行).查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:解答题
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率.
(1)(2) 【解析】试题分析:因为此题需要三步完成,所以画出树状图求解即可,注意要做到不重不漏. 试题解析:(1)画树状图如下: 总共有27种结果,每种结果出现的可能性相同.其中,三辆车全部同向而行的结果有3种,(7分)∴P(三辆车全部同向而行)=; (2)由(1)中树状图可知至少有两辆车向左转的结果有7种, ∴P(至少有两辆车向左转)=.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:填空题
从甲、乙、丙、丁4名三好学生中随机抽取2名学生担任升旗手,则抽取的2名学生是甲和乙的概率为 ________.
【解析】试题分析:随机抽取的所有可能情况为:甲乙;甲丙;甲丁;乙丙;乙丁;丙丁六种情况,则符合条件的只有一种情况,则P(抽取的2名学生是甲和乙)=1÷6=.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:解答题
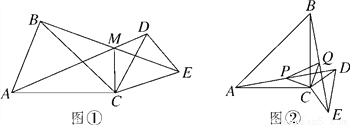
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
甲、乙两人同时从A地出发,骑自行车行30千米到B地,甲比乙每小时少走3千米,结果乙先到40分钟。若设乙每小时走x千米,则可列方程( )
A. 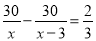 B.
B. 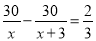 C.
C. 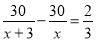 D.
D. 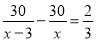
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com