
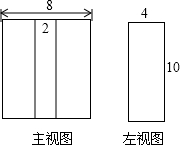
 如图是一个底面为等腰梯形的直四棱柱的主视图和左视图,根据图中的数据求该直四棱柱的侧面积和表面积.
如图是一个底面为等腰梯形的直四棱柱的主视图和左视图,根据图中的数据求该直四棱柱的侧面积和表面积. 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
 (2012•无锡)如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(2012•无锡)如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
(2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是一个水果大棚的立体图,是一个两底面是腰长和底边分别为5m和8m的等腰三角形,侧棱长度为20m的直三棱柱.现在用塑料薄膜覆盖,则至少需
如图是一个水果大棚的立体图,是一个两底面是腰长和底边分别为5m和8m的等腰三角形,侧棱长度为20m的直三棱柱.现在用塑料薄膜覆盖,则至少需查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一个水果大棚的立体图,是一个两底面是腰长和底边分别为5m和8m的等腰三角形,侧棱长度为20m的直三棱柱.现在用塑料薄膜覆盖,则至少需________平方米的塑料薄膜.
如图是一个水果大棚的立体图,是一个两底面是腰长和底边分别为5m和8m的等腰三角形,侧棱长度为20m的直三棱柱.现在用塑料薄膜覆盖,则至少需________平方米的塑料薄膜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com