
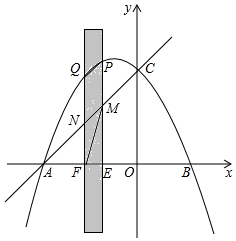
 如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.分析 (1)设抛物线为y=a(x+5)(x-3),把点(0,5)代入即可解决问题.
(2)作FG⊥AC于G,设点F坐标(m,0),根据sin∠AMF=$\frac{FG}{FM}$=$\frac{\sqrt{10}}{10}$,列出方程即可解决问题.
(3))①当MN是对角线时,设点F(m,0),由QN=PM,列出方程即可解决问题.②当MN为边时,设点Q(m,-$\frac{1}{3}$m2-$\frac{2}{3}$m+5)则点P(m+1,-$\frac{1}{3}$m2-$\frac{2}{3}$m+6),代入抛物线解析式,解方程即可.
解答 解:(1)∵抛物线与x轴交于点A(-5,0),B(3,0),
∴可以假设抛物线为y=a(x+5)(x-3),把点(0,5)代入得到a=-$\frac{1}{3}$,
∴抛物线的解析式为y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+5.
(2)作FG⊥AC于G,设点F坐标(m,0),
则AF=m+5,AE=EM=m+6,FG=$\frac{\sqrt{2}}{2}$(m+5),FM=$\sqrt{E{F}^{2}+E{M}^{2}}$=$\sqrt{1+(m+6)^{2}}$,
∵sin∠AMF=$\frac{\sqrt{10}}{10}$,
∴$\frac{FG}{FM}$=$\frac{\sqrt{10}}{10}$,
∴$\frac{\frac{\sqrt{2}}{2}(m+5)}{\sqrt{1+(m+6)^{2}}}$=$\frac{\sqrt{10}}{10}$,整理得到2m2+19m+44=0,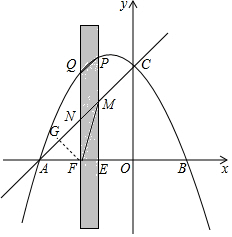
∴(m+4)(2m+11)=0,
∴m=-4或-5.5(舍弃),
∴点Q坐标(-4,$\frac{7}{3}$).
(3)①当MN是对角线时,点M在y轴的右侧,设点F(m,0),
∵直线AC解析式为y=x+5,
∴点N(m,m+5),点M(m+1,m+6),
∵QN=PM,
∴-$\frac{1}{3}$m2-$\frac{2}{3}$m+5-m-5=m+6-[-$\frac{1}{3}$(m+1)2-$\frac{2}{3}$(m+1)+5],
解得m=-3+$\sqrt{6}$或-3-$\sqrt{6}$(舍弃),
此时M(-2+$\sqrt{6}$,3+$\sqrt{6}$),
当MN是对角线时,点N在点A的左侧时,设点F(m,0).
∴m+5-(-$\frac{1}{3}$m2-$\frac{2}{3}$m+5)=[-$\frac{1}{3}$(m+1)2-$\frac{2}{3}$(m+1)+5]-(m+6),
解得m=-3-$\sqrt{6}$或-3+$\sqrt{6}$(舍弃),
此时M(-2-$\sqrt{6}$,3-$\sqrt{6}$)
②当MN为边时,设点Q(m,-$\frac{1}{3}$m2-$\frac{2}{3}$m+5)则点P(m+1,-$\frac{1}{3}$m2-$\frac{2}{3}$m+6),
∵NQ=PM,
∴-$\frac{1}{3}$m2-$\frac{2}{3}$m+6=-$\frac{1}{3}$(m+1)2-$\frac{2}{3}$(m+1)+5,
解得m=-3.
∴点M坐标(-2,3),
综上所述以点P,Q,M,N为顶点的四边形是平行四边形时,点M的坐标为(-2,3)或(-2+$\sqrt{6}$,3+$\sqrt{6}$)或(-2-$\sqrt{6}$,3-$\sqrt{6}$).
点评 本题考查二次函数综合题、三角函数、勾股定理等知识,解题的关键是学会待定系数法确定函数解析式,学会分类讨论,用方程的思想解决问题,属于中考压轴题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:填空题
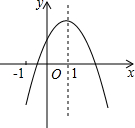 二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是P>Q.
二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是P>Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
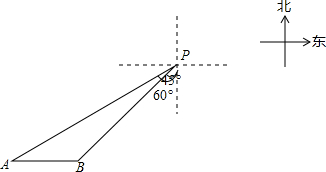 一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为$\sqrt{7}$.
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com