练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示,在△ABC中,BC=AC,BE=AE,则由“SSS”可以判定( )

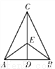
    A. △ACD≌△BCD B. △ADE≌△BDE C. △ACE≌△BCE D. 以上都对

    C 【解析】试题分析：三条边对应相等，BC=AC,BE=AE,CE=CE.所以△ACE≌△BCE，故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

    已知矩形ABCD的AB=2BC，在CD上取点E，使AE=EB，那么∠EBC等于（ ）．

    A. 60° B. 45° C. 30° D. 15°

    B 【解析】作EM⊥AB于M ， ∵AE=BE， ∴M为AB中点 ， ∵AB=2BC， ∴AM=BM=EM ， ∴∠MBE=∠MEB=45°， ∴∠EBC=45°， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 25.1.1随机事件 测试 题型：填空题

    为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,“某运动员被抽到”这一事件是____事件,抽到的可能性为____.

    随机 【解析】根据随机事件的性质可得，因为为了了解参加某运动会的2000名运动员的年龄情况，从中抽查了100名运动员的年龄，所以在2000名运动员抽查100名运动员，所以这一事件为随机事件，且抽到的可能性为100÷2000=. 故答案为：随机， .

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型：解答题

    如图所示,DE⊥AC,BF⊥AC,垂足分别为E,F, DE=BF,AF=CE.求证:AB∥CD.

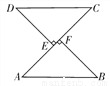
    证明见解析 【解析】试题分析：由题可得，边角边，∆ABF?∆CDE,所以,由平行线的判定方法得AB∥CD. ∵DE⊥AC,BF⊥AC, ∴∠DEC=∠BFA=90°. 在△ABF和△CDE中, ∴△ABF≌△CDE(SAS). ∴∠A=∠C.∴AB∥CD.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型：单选题

    如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）

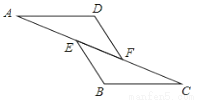
    A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC

    B 【解析】试题分析：求出AF=CE，再根据全等三角形的判定定理判断即可．∵AE=CF，∴AE+EF=CF+EF，∴AF=CE，A、∵在△ADF和△CBE中，∠A=∠C，AF=CE，∠AFD=∠CEB，∴△ADF≌△CBE（ASA），正确，故本选项错误；B、根据AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；C、∵在△ADF和△CBE中，AF=CE，...

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册13.4课题学习 最短路径问题同步练习题 题型：解答题

    已知，如图所示，甲、乙、丙三个人做传球游戏，游戏规则如下：甲将球传给乙，乙将球立刻传给丙，然后丙又立刻将球传给甲．若甲站在∠AOB内的P点，乙站在OA上，丙站在OB上，并且甲、乙、丙三人的传球速度相同．问乙和丙必须站在何处，才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少？

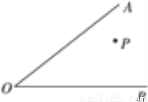
    见解析 【解析】试题分析：分别作出点P关于OA、OB的对称点P1、P2，连接P1P2与OA、OB的交点即为乙、丙的位置. 试题解析：如图所示，(1)分别作点P关于OA，OB的对称点P1，P2， (2)连接P1P2，与OA，OB分别相交于点M，N， 因为乙站在OA上，丙站在OB上，所以乙必须站在OA上的M处，丙必须站在OB上的N处才能使传球所用时间最少．

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图，△ABC的周长为19cm，AC的垂直平分线DE交AC于点E，E为垂足，AE=3cm，则△ABD的周长为________．

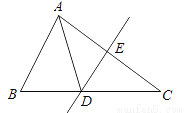
    13cm． 【解析】试题分析：根据垂直平分线的性质计算．△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC．∵AC的垂直平分线DE交BC于D，E为垂足，∴AD=DC，AC=2AE=6cm，∵△ABC的周长为19cm，∴AB+BC=13cm，∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm． 故答案为：13cm．

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离，即|x|=|x﹣0|，也就是说|x|表示在数轴上数x与数0对应点之间的距离；这个结论可以推广为：|x﹣y|表示在数轴上数x、y对应点之间的距离；在解题中，我们常常运用绝对值的几何意义．

    ①解方程|x|=2，容易看出，在数轴上与原点距离为2的点对应的数为±2，即该方程的解为x=±2．

    ②在方程|x﹣1|=2中，x的值就是数轴上到1的距离为2的点对应的数，显然x=3或x=﹣1．

    ③在方程|x﹣1|+|x+2|=5中，显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值，在数轴上1和﹣2的距离为3，满足方程的x的对应点在1的右边或﹣2的左边．若x的对应点在1的右边，由图示可知，x=2；同理，若x的对应点在﹣2的左边，可得x=﹣3，所以原方程的解是x=2或x=﹣3．根据上面的阅读材料，解答下列问题：

    (1)方程|x|=5的解是_______________．

    （2）方程|x﹣2|=3的解是_________________．

    （3）画出图示，解方程|x﹣3|+|x+2|=9．

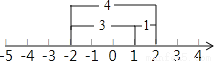
    （1）x=5或-5 ；（2）x=5或-1；（3）x=5或-4. 【解析】试题分析： （1）由于|x|=5表示在数轴上数x与数0对应点之间的距离，所以x=±5； （2）由于|x-2|=3中，x的值就是数轴上到2的距离为3的点对应的数，显然x=5或-1； （3）方程|x-3|+|x+2|=9表示数轴上与3和-2的距离之和为9的点对应的x值，在数轴上3和-2的距离为5，满足方程的...

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：单选题

    如图是小明从学校到家行进的路程 s(米)与时间 t(分)的函数图象，观察图象，从 中得到如下信息，其中不正确的是( )

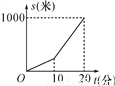
    A. 学校离小明家 1000 米

    B. 小明用了 20 分钟到家

    C. 小明前 10 分钟走了路程的一半

    D. 小明后 10 分钟比前 10 分钟走得快

    C 【解析】由图象的纵坐标可以看出学校离小明家1000米，故A正确，不符合题意；由图象的横坐标可以看出小明用了20到家，故B正确，不符合题意；由图象的纵横坐标可以看出，小明前10分钟走的路程较少，故C错误，符合题意；由图象的纵横坐标可以看出，小明后10分钟比前10分钟走得快，故D正确，不符合题意， 故选C.

    查看答案和解析>>

    同步练习册答案