练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，过正方形的顶点A作对角线BD的平行线，在这条直线上取点E，使BE=BD，且BE与AD交于点F，求证：DE=DF．
    证明：过E作EG⊥BD于G，连接AC，交BD于O点，
    则EG=AC一BD．  
    而BD=BE，
    ∴EG=BE，
    ∴∠EBD=30°．    
    ∴∠BED=∠BDE=75°.    
    而∠BDA=45°，
    ∴∠ADE= 30°.    
    ∴∠EFD=75°,∠EFD=∠FED.    
    ∴DE=DF．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    16、如图所示，以正方形ABCD的对角线AC为边作等边三角形ACE，过点E作EF⊥AD，交AD的延长线于F，则∠DEF=
    45
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，过点A（a，0）（a＞0）且平行于y轴的直线分别与抛物线y=x2及y=
    14
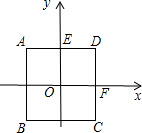    x2交于C、B精英家教网两点．
    （1）求点C、B的坐标；
    （2）求线段AB与BC的比；
    （3）若正方形BCDE的一边DE与y轴重合，求此正方形BCDE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图所示，以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系，若正方形的边长为4．
    （1）求过B、E、F三点的二次函数的解析式；
    （2）求此抛物线的顶点坐标．（先转化为点的坐标，再求函数解析式）

    查看答案和解析>>

    科目：初中数学 来源：2006年山东省临沂市初中毕业生学业考试数学试题(非课改实验区) 题型：059

    已知正方形ABCD．

    (1)如图，E是AD上一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H，求证：BE＝GH；

    (2)如图，过正方形ABCD内任意一点作两条互相垂直的直线，分别交AD、BC于点E、F，交AB、CD于点G、H，EF与GH相等吗？请写出你的结论；

    (3)当点O在正方形ABCD的边上或外部时，过点O作两条互相垂直的直线，被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗？其中一种情形如图所示，过正方形ABCD外一点O作互相垂直的两条直线m、n，m与AD、BC的延长线分别交于点E、F，n与AB、DC的延长线分别交于点G、H，试就该图对你的结论加以证明．

    查看答案和解析>>

    同步练习册答案