
���� ��1�����ȸ������⻭����״ͼ������״ͼ���С�����п���ѡ��ķ�ʽ��
��2�������ɣ�1���е���״ͼ���������С����һ������ľ���ǡ������ѵ������Ȼ�����ø��ʹ�ʽ��⼴����ô𰸣�
��� �⣺��1���б������£�
���� ���� | D | E | F | G |
| A | ��A��D�� | ��A��E�� | ��A��F�� | ��A��G�� |
| B | ��B��D�� | ��B��E�� | ��B��F�� | ��B��G�� |
| C | ��C��D�� | ��C��E�� | ��C��F�� | ��C��G�� |
���� ���⿼��������б�������״ͼ������ʣ�ע����״ͼ�����б������Բ��ظ�����©���г����п��ܵĽ�����б����ʺ���������ɵ��¼�����״ͼ���ʺ�����������������ɵ��¼���ע�����=������������������֮�ȣ�


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
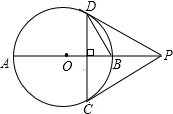 ��֪AB�ǡ�O��ֱ����P��AB�ӳ�����һ�㣬PC�С�O��C��CD��AB����O����һ��D������PD��
��֪AB�ǡ�O��ֱ����P��AB�ӳ�����һ�㣬PC�С�O��C��CD��AB����O����һ��D������PD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
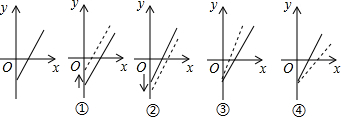
| A�� | �ڣ��� | B�� | �٣��� | C�� | �٣��� | D�� | �ܣ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
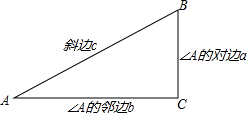 ��ͼ����Rt��ABC�У���C=90�㣬��A����B����C�ĶԱ߷ֱ���a��b��c�����ǰѡ�A���ڱ���б�ߵıȽ�����A�����ң�����cosA����cosA=$\frac{b}{c}$����c=2��a=1ʱ����cosA��
��ͼ����Rt��ABC�У���C=90�㣬��A����B����C�ĶԱ߷ֱ���a��b��c�����ǰѡ�A���ڱ���б�ߵıȽ�����A�����ң�����cosA����cosA=$\frac{b}{c}$����c=2��a=1ʱ����cosA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
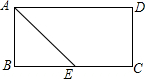 �ھ���ABCD�У�AD=5��AB=3��AEƽ�֡�BAD��BC���ڵ�E�����߶�BE��EC�ij��ȷֱ�Ϊ��������
�ھ���ABCD�У�AD=5��AB=3��AEƽ�֡�BAD��BC���ڵ�E�����߶�BE��EC�ij��ȷֱ�Ϊ��������| A�� | 2��3 | B�� | 3��2 | C�� | 4��1 | D�� | 1��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com