解:(1)设经过x秒钟,使△PBQ的面积为8cm
2,
BP=6-x,BQ=2x,
∵∠B=90°,
∴

BP×BQ=8,
∴

×(6-x)×2x=8,
∴x
1=2,x
2=4,
答:经过2或4秒钟,使△PBQ的面积为8cm
2.
(2)设y秒后PQ的长为3

厘米,
则BP=6-y,BQ=2y,
(6-y)
2+(2y)
2=(3

)
2,
解得y
1=3,y
2=-

(舍去),
答:3秒后PQ的长为3

厘米;
(3)解:设经过a秒钟,使△PBQ与△ABC相似,
∵∠B=∠B,
第一种情况:当 BP:AB=BQ:BC时,△PBQ与△ABC相似,
∴(6-a):6=2a:8,
解得:a=2.4,
第二种情况:当 BP:BC=BQ:AB时,△PBQ与△ABC相似,
∴(6-a):8=2a:6,
∴a=
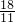
,
答:如果点P、Q分别从A、B同时出发,经过2.4或
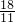
秒钟,使△PBQ与△ABC相似.
分析:(1)设经过x秒钟,使△PBQ的面积为8cm
2,得到BP=6-x,BQ=2x,根据三角形的面积公式得出方程

×(6-x)×2x=8,求解即可;
(2)设y秒后PQ的长为3

厘米,则BP=6-y,BQ=2y,根据勾股定理得出方程 (6-y)
2+(2y)
2=(3

)
2,求解即可;
(3)设经过a秒钟,使△PBQ与△ABC相似,根据两边成比例并且夹角相等的两三角形相似得到第一种情况 BP:AB=BQ:BC和第二种情况 BP:BC=BQ:AB,代入求出即可.
点评:本题考查了相似三角形的判定以及一元二次方程的应用、三角形面积的求法,是中考压轴题,难度较大.

 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别从A、B同时出发,问:
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别从A、B同时出发,问: 厘米?
厘米? BP×BQ=8,
BP×BQ=8, ×(6-x)×2x=8,
×(6-x)×2x=8, 厘米,
厘米, )2,
)2, (舍去),
(舍去), 厘米;
厘米;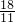 ,
,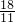 秒钟,使△PBQ与△ABC相似.
秒钟,使△PBQ与△ABC相似. ×(6-x)×2x=8,求解即可;
×(6-x)×2x=8,求解即可; 厘米,则BP=6-y,BQ=2y,根据勾股定理得出方程 (6-y)2+(2y)2=(3
厘米,则BP=6-y,BQ=2y,根据勾股定理得出方程 (6-y)2+(2y)2=(3 )2,求解即可;
)2,求解即可;

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为