
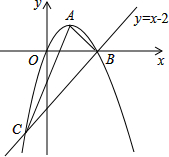
 如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.分析 (1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)先求出AB,BC,AC,利用勾股定理的逆定理可得出△ABC是直角三角形,最后利用三角形的面积即可求出内切圆的半径;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得$\frac{MN}{AB}=\frac{ON}{BC}$或$\frac{MN}{BC}=\frac{ON}{AB}$,可求得N点的坐标.
解答 解:
(1)∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x-1)2+1,
又抛物线过原点,
∴0=a(0-1)2+1,解得a=-1,
∴抛物线解析式为y=-(x-1)2+1,
即y=-x2+2x,
联立抛物线和直线解析式可得$\left\{\begin{array}{l}{y=-{x}^{2}+2x}\\{y=x-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$,
∴B(2,0),C(-1,-3);
(2)由(1)知,B(2,0),C(-1,-3);
∵A(1,1),
∴AB=$\sqrt{(2-1)^{2}+(0-1)^{2}}$=$\sqrt{2}$,BC=$\sqrt{(2+1)^{2}+(0+3)^{2}}$=3$\sqrt{2}$,AC=$\sqrt{(1+1)^{2}+(1+3)^{2}}$=2$\sqrt{5}$,
∴AB2+BC2=AC2
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
∴r=$\frac{AB+BC-AC}{2}$=$\frac{\sqrt{2}+3\sqrt{2}-2\sqrt{5}}{2}$=2$\sqrt{2}$-$\sqrt{5}$;
(3)假设存在满足条件的点N,设N(x,0),则M(x,-x2+2x),
∴ON=|x|,MN=|-x2+2x|,
由(2)知,AB=$\sqrt{2}$,BC=3$\sqrt{2}$,
∵MN⊥x轴于点N,
∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时,有$\frac{MN}{AB}=\frac{ON}{BC}$或$\frac{MN}{BC}=\frac{ON}{AB}$,
①当$\frac{MN}{AB}=\frac{ON}{BC}$时,
∴$\frac{|-{x}^{2}+2x|}{\sqrt{2}}=\frac{|x|}{3\sqrt{2}}$,即|x||-x+2|=$\frac{1}{3}$|x|,
∵当x=0时M、O、N不能构成三角形,
∴x≠0,
∴|-x+2|=$\frac{1}{3}$,
∴-x+2=±$\frac{1}{3}$,解得x=$\frac{5}{3}$或x=$\frac{7}{3}$,
此时N点坐标为($\frac{5}{3}$,0)或($\frac{7}{3}$,0);
②当$\frac{MN}{BC}=\frac{ON}{AB}$,时,
∴$\frac{|-{x}^{2}+2x|}{3\sqrt{2}}=\frac{|x|}{\sqrt{2}}$,
即|x||-x+2|=3|x|,
∴|-x+2|=3,
∴-x+2=±3,
解得x=5或x=-1,
此时N点坐标为(-1,0)或(5,0),
综上可知存在满足条件的N点,其坐标为($\frac{5}{3}$,0)或($\frac{7}{3}$,0)或(-1,0)或(5,0).
点评 本题为二次函数的综合应用,涉及知识点有待定系数法、图象的交点问题、直角三角形的判定、勾股定理及逆定理、相似三角形的性质及分类讨论等.在(1)中注意顶点式的运用,在(3)中设出N、M的坐标,利用相似三角形的性质得到关于坐标的方程是解题的关键,注意相似三角形点的对应.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
 完成下面的证明(下划线内补全证明过程,括号内填写推理的依据).
完成下面的证明(下划线内补全证明过程,括号内填写推理的依据).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
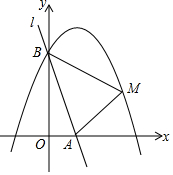 如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.
如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
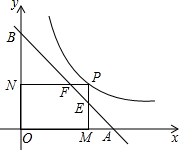 如图,P为反比例函数y=$\frac{3}{2x}$(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=-x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AF•BE的值为3.
如图,P为反比例函数y=$\frac{3}{2x}$(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=-x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AF•BE的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. | Q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com