
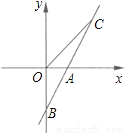
��ͼ��ֱ��AB��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0����2����
��1����ֱ��AB�Ľ���ʽ��
��2����ֱ��AB�ϵĵ�C�ڵ�һ���ޣ���S��BOC=2�����C�����꣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
�����⣺ (1) 4.2��(��5.8)��3 (2) ��22��3������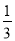 ����|��5|��
����|��5|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
����ͼ���У������ĶԳ�ͼ�ε��ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ������
�̵�Ϊ�˶�ij����Ʒ������������Ϊ3Ԫ����Ʒ�������з�ʽ�Ż����ۣ���������5������ԭ�۸����һ���Թ���5�����ϣ��������ִ���ۣ������27ԪǮ�������Թ������Ʒ�ļ�����_____��
10 ���������������������Թ���x����������Ʒ�� 3��5+��x-5����3��0.8��27 ���x��10�� �������Թ������Ʒ�ļ�����10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��������������ͼ������3��2���������ͼ��һ�������㣨������
A. ��2����3�� B. (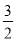 ,-1) C. ����1��1�� D. ��2����2��
,-1) C. ����1��1�� D. ��2����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������2017-2018��ʦ�����꼶���ϣ���ѧ��ĩģ���Ծ� ���ͣ������
��֪x��yΪʵ������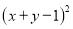 ��
��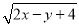 ��ֵ��Ϊ�෴������
��ֵ��Ϊ�෴������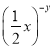 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������2017-2018��ʦ�����꼶���ϣ���ѧ��ĩģ���Ծ� ���ͣ������
��ֱ֪�����������߳��ֱ�Ϊ3cm��4cm����������߳�Ϊ_______________��
5 cm��cm ���������������Ϊxcm�� ��1����4��ֱ�DZߣ��������x��б�ߣ��ɹ��ɶ����ã�32+42=x2������x=5�� ��2����4��б�ߣ��������xΪֱ�DZߣ��ɹ��ɶ����ã�32+x2=42������x=�� ���ϵ����ߵij�Ϊ5cm��cm�� �ʴ�Ϊ��5cm��cm.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ� ���ͣ������
�Ȼ����������ʽ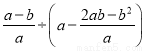 ��ֵ������
��ֵ������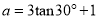 ��
�� 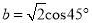 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�����к���ѧУ2017-2018ѧ�����꼶�ϲ���ѧ���в��Ծ������𰸣� ���ͣ������
�Ƿ��������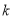 ��ʹ����
��ʹ����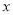 �ķ���
�ķ���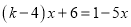 �������⣿�����ڣ������
�������⣿�����ڣ������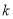 ��ֵ��������˷��̵Ľ⣻�������ڣ���˵�����ɣ�
��ֵ��������˷��̵Ľ⣻�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com