
已知:如图,正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为x,求y与x之间的函数关系式.

|
解:∵四边形ABCD是正方形, ∴AB=AD,∠B=∠D=90°. 又∵AE=AF, ∴△ABE≌△ADF, ∴BE=DF. ∵BC=CD, ∴FC=EC=x, ∴BE=DF=4-x. ∴S△AEF-AB2-2×S△AEF-S△ECF =42-2× =- ∵E在BC边上运动,A、E、F要构成三角形 ∴0<x≤4 ∴y与x之间的函数关系式是 y=- 思路点拨:△AEF的面积等于正方形的面积,减去△ABE、△ADF、△EFC三个三角形的面积,所以只要用变量x表示这三个三角形的面积即可. 评注:本题若不采用割补法的思想来求三角形AEF的面积,而直接想方设法求三角形AEF的面积则比较麻烦.另外,在解实际问题时,一定要考虑自变量x的取值范围. |


科目:初中数学 来源: 题型:
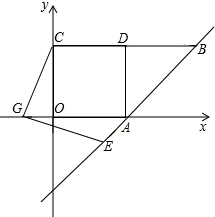
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 32 |
| x |
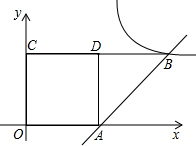
| OG+GF |
| DF |
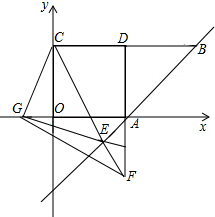
查看答案和解析>>
科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:
 于E,交CD于F.
于E,交CD于F.| 13 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:
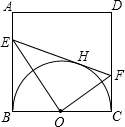
 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com