Question

AB为定⊙O的定弦，但不是直径作⊙O的弦C_iD_i（i=1，2，…1999）使得所有C_iD_i都被弦AB平分于M_i，过C_iD_i作⊙O的切线交于P_i，求证：P₁，P₂，…，P₁₉₉₉共圆．

Answer 1

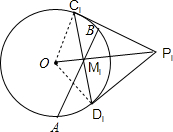
如图，对每个P_i，我们证明：P_i总在△OAB的外接圆上．
连接OC_i，OD_i，由P_iC_i，P_iD_i是切线知：C_i与D_i关于OP_i对称，
由M_i是C_iD_i的中点，所以OP_i过M_i，
由AB与C_iD_i相交于M_i，由相交弦定理，得：
AM_i•BM_i=C_iM_i•D_iM_i（1）
又∠OC_iP_i=∠OD_iP_i=90°
∴O、C_i、D_i、P_i四点共圆．
由相交弦定理，得C_iM_i•D_iM_i=OM_i•P_iM_i（2）
由（1）（2）得AM_i•BM_i=OM_i•P_iM_i，
∴A、O、B、P_i四点共圆．
故每个P_i都在△AOB的外接圆上，因此所有P₁，P₂，P₁₉₉₉共圆．
分析：如图，对每个P_i，我们只要证明P_i总在△OAB的外接圆上即可．连接OC_i，OD_i，由P_iC_i，P_iD_i是切线可以得到C_i与D_i关于OP_i对称，由M_i是C_iD_i的中点，所以OP_i过M_i，由AB与C_iD_i相交于M_i，由相交弦定理可以得到AM_i•BM_i=C_iM_i•D_iM_i（1），又∠OC_iP_i=∠OD_iP_i=90°，可以得到O、C_i、D_i、P_i四点共圆．然后利用同样方法可以证明A、O、B、P_i四点共圆，这样可以证明题目的结论．
点评：此题主要考查了四点共圆的问题，也综合运用了切线长定理、三角形的外心的性质以及证明四点共圆的方法．比较复杂，解题时要细心和耐心．