科目：初中数学 来源：江苏省2018届九年级上学期期中考试数学试卷 题型：单选题
如图，△ABC中，DE∥BC，DE=1，AD=2，DB=3，则BC的长是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源：江苏省东台市第二联盟2018届九年级12月月考数学试卷 题型：填空题
如图，在平面直角坐标系中，菱形OABC 的顶点 A 在 x 轴正半轴上，顶点 C 的坐标为（4，3），D是抛物线 y=﹣x2+6x上一点，且在x轴上方，则△BCD 面积的最大值为__________
查看答案和解析>>
科目：初中数学 来源：江苏省东台市第二联盟2018届九年级12月月考数学试卷 题型：单选题
如图，在△ABC中，AD⊥BC于D，AD=BC=12，点P在AB上，且PQ∥AD交BC于点Q，PM∥BC交AC于点M，若PM=2PQ，则PM等于（ ）
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目：初中数学 来源：山东省淄博市2017届九年级下学期期中考试数学试卷 题型：解答题
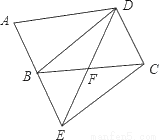
如图，将?ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．
（1）求证：△BEF≌△CDF；
（2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．
【答案】（1）证明见解析；（2）证明见解析．
【解析】试题分析：（1）证出BE=DC，根据平行四边形的判定与性质得到四边形BECD为平行四边形；
（2）欲证明四边形BECD是矩形，只需推知BC=ED即可．
试题解析：（1）∵四边形ABCD是平行四边形
∴AB=CD，AB∥CD，
又∵AB=BE，
∴BE=DC，
又∵AE∥CD，
∴四边形BECD为平行四边形；
（2）由（1）知，四边形BECD为平行四边形
∴OD=OE，OC=OB，
∵四边形ABCD为平行四边形，
∴∠A=∠BCD
又∵∠BOD=2∠A，∠BOD=∠OCD+∠ODC，
∴∠OCD=∠ODC，
∴OC=OD，
∴OC+OB=OD+OE，即BC=ED，
∴平行四边形BECD为矩形．
【点睛】题考查了平行四边形的性质和判定，矩形的判定，平行线的性质，全等三角形的性质和判定，三角形的外角性质等知识点的综合运用，难度较大．
【题型】解答题
【结束】
23
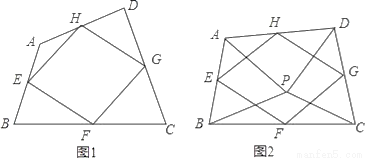
我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
查看答案和解析>>
科目：初中数学 来源：福建省2016-2017学年八年级下学期期中考试数学试卷 题型：解答题
已知直线
与
轴交于点A(－6，0)，与
轴交于点B.
（1）求b的值；
（2）把△AOB绕原点O顺时针旋转90°后，点A落在
轴的
处，点B若在
轴的
处；
①求直线
的函数关系式；
②设直线AB与直线
交于点C，长方形PQMN是△
的内接长方形，其中点P，Q在线段
上，点M在线段
上，点N在线段AC上.若长方形PQMN的两条邻边的比为1∶2，试求长方形PQMN的周长.
查看答案和解析>>
科目：初中数学 来源：湖北省孝感市云梦县2018届九年级上学期期中考试数学试卷（WORD版） 题型：单选题
若方程ax2+bx+c=0的两个根是﹣4和2，那么二次函数y=ax2+bx+c的图象的对称轴是直线（ ）
A. x=﹣2 B. x=﹣1 C. x=0 D. x=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是同类二次根式的是（ ）
B. 
C. 
D. 
