
在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源:2016-2017学年江苏泰州中学附中八年级上期中数学试卷(解析版) 题型:选择题
一个正方形的面积是15,估计它的边长大小在( ).
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:解答题
在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程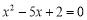 ,操作步骤是:
,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点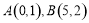 ;
;
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点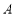 ,另一条直角边恒过点
,另一条直角边恒过点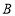 ;
;
第三步:在移动过程中,当三角板的直角顶点落在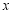 轴上点
轴上点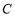 处时,点
处时,点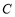 的横坐标
的横坐标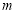 即为该方程的一个实数根(如图1);
即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在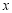 轴上另—点
轴上另—点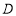 处时,点
处时,点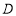 的横坐标
的横坐标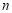 即为该方程的另一个实数根.
即为该方程的另一个实数根.
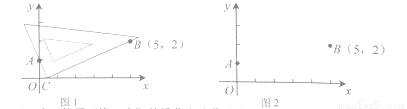
(1)在图2中,按照“第四步”的操作方法作出点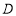 (请保留作出点
(请保留作出点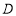 时直角三角板两条直角边的痕迹);
时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的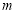 就是方程
就是方程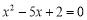 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程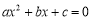
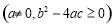 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当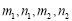 与
与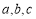 之间满足怎样的关系时,点
之间满足怎样的关系时,点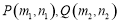 就是符合要求的—对固定点?
就是符合要求的—对固定点?
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:解答题
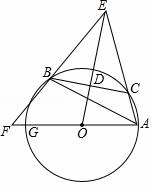
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:填空题
一个仅装有球的不透明布袋里共有3个球(只有颜色不同),其中2个是红球,1个是白球,从中任意摸出一个球,记下颜色后放回,搅匀,再任意摸出一个球,则两次摸出都是红球的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com