解:(1)∵AB和AG在同一条直线上,
∴∠EAB=90°,
∵AF、AC分别是正方形的对角线,
∴∠EAF=∠BAC=45°,
∴∠FAC=∠FAE+∠EAB+∠BAC=180°,
故C、A、F在同一条直线上.
(2)由题意得,OA=AB=1,
结合直角坐标系可得点C的坐标为(2,-1),点F的坐标为(-1,2),
设过点C的反比例函数关系式为y=

,将点C代入可得:-1=

,
解得:k=-2,即反比例函数关系式为y=-

,
将点F(-1,2)代入可得:2=-

,从而可得点F也在经过点C的反比例函数上.
即点C、点F是否在同一个反比例函数的图象上,这个反比例函数为y=-

.
(3)由题意得,OA=AB=m,
结合直角坐标系可得点C的坐标为(2m,-m),点F的坐标为(-m,2m),
设过点C的反比例函数关系式为y=

,将点C代入可得:-m=

,
解得:k=-2m
2,即反比例函数关系式为y=-
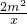
,
将点F(-m,2m)代入可得:2m=-
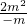
,从而可得点F也在经过点C的反比例函数上.
即点C、点F是否在同一个反比例函数的图象上,这个反比例函数为y=-
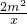
.
分析:(1)根据AB和AG在同一条直线上可求出∠EAB的度数,再由正方形的性质可得∠EAF=∠BAC=45°,故根据∠FAC为平角可得出C、A、F三点共线;
(2)根据方格坐标纸,可得出点C、点F的坐标,根据点C的坐标确定反比例函数的关系式,然后代入点F的坐标进行判断即可;
(3)用m表示出点C、点F的坐标,然后根据点C的坐标确定反比例函数的关系式,然后代入点F的坐标进行判断即可;
点评:本题考查了三点共线的证明、点的坐标与线段长度之间的转换及待定系数法求反比例函数解析式的知识,涉及的知识点较多,解答最后两问的关键是在方格坐标纸上得出点C及点F的坐标.


 ,将点C代入可得:-1=
,将点C代入可得:-1= ,
, ,
, ,从而可得点F也在经过点C的反比例函数上.
,从而可得点F也在经过点C的反比例函数上. .
. ,将点C代入可得:-m=
,将点C代入可得:-m= ,
,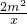 ,
,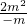 ,从而可得点F也在经过点C的反比例函数上.
,从而可得点F也在经过点C的反比例函数上.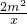 .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案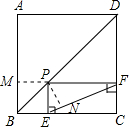 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF; ③△APD一定是等腰三角形; ④∠PFE=∠BAP;⑤PD=
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF; ③△APD一定是等腰三角形; ④∠PFE=∠BAP;⑤PD=