Question

已知一个直角三角形AOB，其中∠AOB=90°，OA=2，OB=4．将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB交于点C，与边AB交于点D．

（1）如图1，若折叠后使点B与点O重合，则点D的坐标为______；
（2）如图2，若折叠后使点B与点A重合，求点C的坐标；
（3）如图3，若折叠后点B落在边OA上的点为B′，设OB′=x，OC=y，试写出y关于x的函数解析式．

Answer 1

解：（1）由折叠的性质 可知，BC=OC，CD⊥OB，
则CD为△OAB的中位线，所以D（1，2），
故答案为：（1，2）；

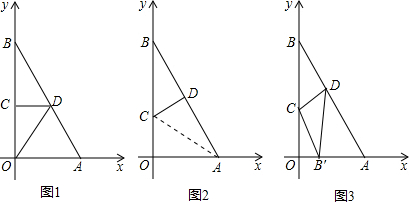
（2）如图2，折叠后点B与点A重合，则△ACD≌△BCD，
设C点坐标为（0，m）（m＞0），则BC=OB-OC=4-m，于是AC=BC=4-m，
在Rt△AOC中，由勾股定理，得AC²=OC²+OA²，即（4-m）²=m²+2²，
解得m=，所以C（0，）；

（3）如图3，折叠后点BB落在边OA上的点为B′，则△B′CD≌△BCD，
依题意设OB′=x，OC=y，则B′C=BC=OB-OC=4-y，
在Rt△B′OC中，由勾股定理，得B′C²=OC²+OB′²，即（4-y）²=y²+x²，即y=-x²+2，
由点B′在边OA上，有0≤x≤2，
所以，函数解析式为y=-x²+2（0≤x≤2）．
分析：（1）由CD为△OAB的中位线，可求D点坐标；
（2）设OC=m，由折叠的性质可知，△ACD≌△BCD，则BC=AC=4-m，OA=2，在Rt△AOC中，利用勾股定理求m的值；
（3）由折叠的性质可知，△B′CD≌△BCD，依题意设OB′=x，OC=y，则B′C=BC=OB-OC=4-y，在Rt△B′OC中，由勾股定理，建立y与 x之间的函数关系式．
点评：本题考查了一次函数的综合运用．关键是由折叠的性质得出全等三角形，在直角三角形中，利用勾股定理建立等式，解方程或得出函数关系式．