
如图所示,已知AD是∠BAC的平分线,DE∥AB,DE=AC,AD≠EC.
(1)求证四边形ADCE是等腰梯形;
(2)若△ADC的周长为16cm,AE=3cm,AC-EC=3cm,求四边形ADCE的周长.

|
证明: (1)∵AB∥ED(已知),∴∠ BAD=∠ADE(两直线平行,内错角相等).又∵∠ BAD=∠CAD(角平分线定义),∴∠ CAD=∠ADE.∴ OA=OD(等角对等边).∵ AC=DE(已知),∴ AC-OA=ED-OD.即 OE=OC,∴∠ OEC=∠OCE(等边对等角).又∵∠ AOD=∠COE(对顶角相等),∴∠ CAD=∠OCE.∴ AD∥CE(内错角相等,两直线平行).而 AD≠CE,∴四边形 ADCE是梯形.又∵∠ CAD=∠ADE,AD=AD,AC=DE,∴△ ADE≌△DAC,∴ AE=DC(全等三角形的对应边相等).∴四边形 ADCE是等腰梯形.解: (2)∵四边形ADCE是等腰梯形,∴ AE=CD=3cm,∴梯形 ADCE的周长=AD+EC+AE+DC=AD+CE+6,而△ADC的周长=AD+DC+AC=16,∴ AD+AC=13.∵ AC-EC=3,∴AD+AC-(AC-EC)=10.即 AD+EC=10.∴梯形 ADCE的周长=10+6=16(cm). |
|
(1) 由角平分线和平行线可得到一些相等的角.如∠OAD=∠ODA.从而有OA=OD,再由AC=DE推出∠OCE=∠OEC,得出结论AD∥CE,因为AD≠CE,所以能证出四边形ADCE是梯形,再由已知条件容易证出△ADE≌△DAC,因此有AE=DC,所以可证出四边形ADCE是等腰梯形.(2) 因为四边形ADCE是等腰梯形,所以由给出条件容易求出四边形ADCF的周长. |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
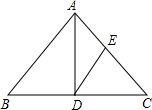 如图所示,已知AD是等腰△ABC底边上的高,且tan∠B=
如图所示,已知AD是等腰△ABC底边上的高,且tan∠B=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com