
如图所示,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,求矩形ABCD中最大正方形与最小正方形的面积之差.

|
解:因为小正方形的面积为4,所以它的边长为2,显然它是最小的正方形,其余正方形的边长是b=a+2,c=b+2=a+4,d=c+2=a+6,可见,边长为d的正方形是矩形ABCD中最大的正方形,于是,最大与最小正方形的面积之差为: (a+6)2-22=(a+6+2)(a+6-2) =(a+8)(a+4) =a2+12a+32 能不能求出a呢,因为长方形中AB=DC,而AB=c+d=a+4+a+6=2a+10,DC=b+2a=a+2+2a=3a+2,所以有:2a+10=3a+2,解得a=8 所以面积之差a2+12a+32=82+12×8+32=192. 说明:巧妙地利用图形的特殊构成,求出各正方形边长是解本题的关键. |


科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
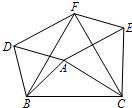 18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
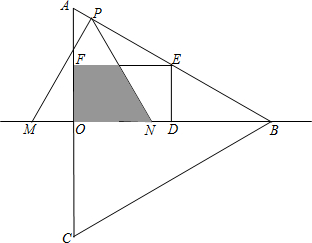 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com