
设a、b、c表示三角形三边的长,它们都是自然数,其中a≤b≤c,如果b=n(n是自然数),试问这样的三角形有多少个?
|
解析:我们先来研究一些特殊情况: (1)设b=n=1,这时b=1,因为a≤b≤c,所以a=1,c可取1,2,3,….若c=1,则得到一个三边都为1的等边三角形;若c≥2,由于a+b=2,那么a+b不大于第三边c,这时不可能由a,b,c构成三角形,可见,当b=n=1时,满足条件的三角形只有一个. (2)设b=n=2,类似地可以列举各种情况如下表.
这时满足条件的三角形总数为:1+2=3. (3)设b=n=3,类似地可得下表.
这时满足条件的三角形总数为:1+2+3=6. 通过上面这些特例不难发现,当b=n时,满足条件的三角形总数为:1+2+3+…+n= 这个猜想是正确的.因为当b=n时,a可取n个值(1,2,3,…,n),对应于a的每个值,不妨设a=k(1≤k≤n).由于b≤c<a+b,即n≤c<n+k,所以c可能取的值恰好有k个(n,n+1,n+2,…,n+k-1).所以,当b=n时,满足条件的三角形总数为:1+2+3+…+n= |


科目:初中数学 来源: 题型:
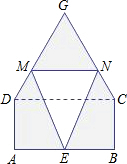 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.查看答案和解析>>
科目:初中数学 来源: 题型:
 下滑动且始终保持和AB平行的伸缩横杆,△EMN是随MN滑动而变化的三角通风窗(阴影部分均不通风).
下滑动且始终保持和AB平行的伸缩横杆,△EMN是随MN滑动而变化的三角通风窗(阴影部分均不通风).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | |
| 多边形2 | 7 | 3 | |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则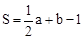 (史称“皮克公式”).
(史称“皮克公式”).
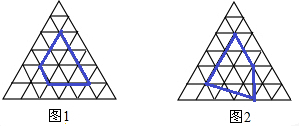
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
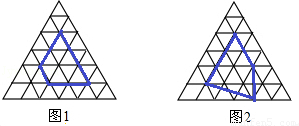
根据图中提供的信息填表:
|
|
格点多边形各边上的格点的个数 |
格点边多边形内部的格点个数 |
格点多边形的面积 |
|
多边形1 |
8 |
1 |
|
|
多边形2 |
7 |
3 |
|
|
… |
… |
… |
… |
|
一般格点多边形 |
a |
b |
S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com