

���� ��1���Ƚⷽ��x2-4x-5=0�õ�A��-1��0����B��5��0��������轻��ʽy=a��x+1����x-5������Ȼ���C������������a���ɣ�
��2����NH��x����H����ͼ1����M��t��0����֤����AMN�ס�ABC���������Ʊȿɱ�ʾ��NH=$\frac{5}{6}$��x+1������S��CMN=S��ACM-S��AMN=-$\frac{5}{12}$x2+$\frac{5}{3}$x+$\frac{25}{12}$��Ȼ�����ö��κ��������ʽ�����⣻
��3����ȷ��D��4��-5������ͼ2��Ȼ��������ۣ���AF��DE������E��0��-5����CD=4���ô�ʱF������Ϊ��3��0����-5��0������EF��AD��AD=EFʱ������ƽ���ı��ε����ʿɵõ���E�͵�D�������껥Ϊ�෴������������y=5ʱ��x=2+$\sqrt{14}$��x=2-$\sqrt{14}$���õ�E������Ϊ��2+$\sqrt{14}$��5����2-$\sqrt{14}$��5����Ȼ�����õ�ƽ�ƵĹ��ɺ�ȷ����ӦF������꣮
��� �⣺��1���ⷽ��x2-4x-5=0��x1=-1��x2=5����A��-1��0����B��5��0����
�������߽���ʽΪy=a��x+1����x-5������
��C��0��-5�������-5=a��1����-5�������a=1��
���������߽���ʽΪy=x2-4x-5��
��2����NH��x����H����ͼ1��
��M��t��0����
��MN��BC��
���AMN�ס�ABC��
��AM��AB=NH��CO������x+1����6=NH��5��
��NH=$\frac{5}{6}$��x+1����
��S��CMN=S��ACM-S��AMN=$\frac{1}{2}$��x+1��•5-$\frac{1}{2}$•��x+1��•$\frac{5}{6}$��x+1��
=-$\frac{5}{12}$x2+$\frac{5}{3}$x+$\frac{25}{12}$
=-$\frac{5}{12}$��x-2��2+$\frac{15}{4}$��
��x=2ʱ����CMN��������ʱM�������Ϊ��2��0����
��3����x=4ʱ��y=x2-4x-5=5����D��4��-5������ͼ2��
��AF��DE����E��0��-5����CD=4������AF=4����ʱF������Ϊ��3��0����-5��0����
��EF��AD��AD=EFʱ�����E�͵�D�������껥Ϊ�෴��������E��������Ϊ5��
��y=5ʱ��x2-4x-5=5�����x1=2+$\sqrt{14}$��x2=2-$\sqrt{14}$����E������Ϊ��2+$\sqrt{14}$��5�������ڵ�A��-1��0������ƽ��5����λ������ƽ��5����λ�õ�D�㣬��E������ƽ��5����λ������ƽ��5����λ�õ�F�㣬��ʱF������Ϊ��7+$\sqrt{14}$��0������E������Ϊ��2-$\sqrt{14}$��5����ͬͬ�������õ���ʱF������Ϊ��7-$\sqrt{14}$��0����
��������������������F��������-5��0������3��0������7-$\sqrt{14}$��0������7+$\sqrt{14}$��0����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ�����������������κ��������ʺ�ƽ���ı��ε����ʣ������ô���ϵ��������κ�������ʽ������������ͼ�����ʣ����������Ʊȼ����߶εij��������÷������۵�˼�������⣮


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
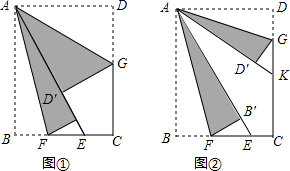
 ��ͼ���ı���ABCD�У�AB��DC����B=90�㣬FΪDC��һ�㣬��FC=AB��EΪAD��һ�㣬EC��AF�ڵ�G��
��ͼ���ı���ABCD�У�AB��DC����B=90�㣬FΪDC��һ�㣬��FC=AB��EΪAD��һ�㣬EC��AF�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
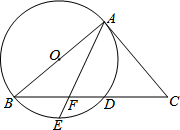 ��ͼ���ԡ�ABC�ı�ABΪֱ������O����BC���ڵ�D����E�ǻ�BD���е㣬����AE��BC�ڵ�F����ACB=2��BAE��
��ͼ���ԡ�ABC�ı�ABΪֱ������O����BC���ڵ�D����E�ǻ�BD���е㣬����AE��BC�ڵ�F����ACB=2��BAE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
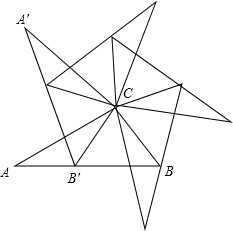 ��ͼ���ڡ�ABC�У��Ե�CΪ��ת���ģ�����ABC��ת����A��B��C��λ�ã�����A�䣬B��ֱ���A��B�Ķ�Ӧ�㣬�ҵ�B����AB���ϣ���������������ת��A��B��C��������������ת�Ĵ�ǡ�ù���һ����ת�Գ�ͼ�Σ�
��ͼ���ڡ�ABC�У��Ե�CΪ��ת���ģ�����ABC��ת����A��B��C��λ�ã�����A�䣬B��ֱ���A��B�Ķ�Ӧ�㣬�ҵ�B����AB���ϣ���������������ת��A��B��C��������������ת�Ĵ�ǡ�ù���һ����ת�Գ�ͼ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com