
如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.

(1)求证:AC平分∠BAD;
(2)若CD=1,AC= ,求⊙O的半径长.
,求⊙O的半径长.
(1)见解析;(2) .
.
【解析】
试题分析:(1)连接OC,由OA=OC得∠ACO=∠CAO,由切线的性质得出OC⊥CD,根据垂直于同一直线的两直线平行得到AD∥CO,由平行线的性质得∠DAC=∠ACO,等量代换后可得∠DAC=∠CAO,即AC平分∠BAD.
过点O作OE⊥AC于E.先在Rt△ADC中,由勾股定理求出AD=3,由垂径定理求出AE= ,再根据两角对应相等的两三角形相似证明△AEO∽△ADC,由相似三角形对应边成比例得到
,再根据两角对应相等的两三角形相似证明△AEO∽△ADC,由相似三角形对应边成比例得到 ,求出AO=
,求出AO= ,即⊙O的半径为
,即⊙O的半径为 .
.
试题解析:(1)证明:如图,连接OC,

∵OA=OC,∴∠ACO=∠CAO.
∵CD切⊙O于C,∴OC⊥CD.
又∵AD⊥CD,∴AD∥CO.
∴∠DAC=∠ACO.
∴∠DAC=∠CAO,即AC平分∠BAD.
(2)如图,过点O作OE⊥AC于E.

在Rt△ADC中, ,
,
∵OE⊥AC,∴AE= AC=
AC= .
.
∵∠CAO=∠DAC,∠AEO=∠ADC=90°,
∴△AEO∽△ADC.
∴ ,即
,即 ,
,
∴AO= ,即⊙O的半径为
,即⊙O的半径为 .
.
考点:1.垂径定理的性质;2.相似三角形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
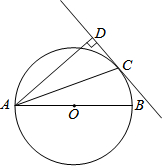 (2013•营口)如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.
(2013•营口)如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.| 10 |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:013
A.![]() ∶1 B.
∶1 B. ![]() ∶2
∶2
C.![]() ∶4 D.
∶4 D. ![]() ∶4
∶4

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁营口卷)数学(解析版) 题型:解答题
如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.

(1)求证:AC平分∠BAD;
(2)若CD=1,AC= ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源:2013年辽宁省营口市中考数学试卷(解析版) 题型:解答题
 如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.
如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D. ,求⊙O的半径长.
,求⊙O的半径长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com