
 +
+ ,其中a为锐角,则:
,其中a为锐角,则: ;
;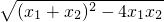 ,以这条线段为底,抛物线与y轴交点纵坐标的绝对值为高即可得到三交点围成的三角形的面积值,然后判断是否小于1即可.
,以这条线段为底,抛物线与y轴交点纵坐标的绝对值为高即可得到三交点围成的三角形的面积值,然后判断是否小于1即可. ,二次函数解析式可写作:y=x2-
,二次函数解析式可写作:y=x2- x=(x-
x=(x- )2-
)2- ;
; ;故①正确.
;故①正确. )x-sina+
)x-sina+ =0,
=0, )2-4×2sina×(-sina+
)2-4×2sina×(-sina+ )=24sin2a+
)=24sin2a+ >0,
>0, ,得:y=
,得:y= x2-(2
x2-(2 +
+ )x-
)x- ,则:
,则: |x1-x2|×
|x1-x2|× =
= ×
×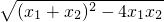 =
= ×
× ≈0.3<1
≈0.3<1 =1+
=1+ >1,
>1, )x-sina+
)x-sina+ =sina(2x2-4x-1)-
=sina(2x2-4x-1)- x+
x+ ;
; 时,抛物线经过定点,且坐标为:(1+
时,抛物线经过定点,且坐标为:(1+ ,-
,- )、(1-
)、(1- ,
, );
);

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
 已知关于x 的一元二次方程(m+2)x2-2x-1=0.
已知关于x 的一元二次方程(m+2)x2-2x-1=0.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| (x2-x1)2+(y2-y1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com