
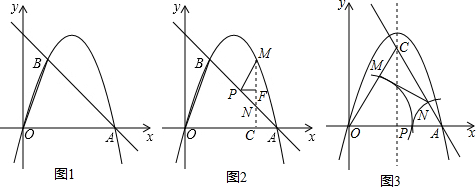
���� ��1�������A��B��������꣬�ٴ���������y=ax2+bx���a��b��ֵ���ɣ�
��2����BD��x���ڵ�D���ӳ�MP��x���ڵ�E����������ɵ�OD=1��BD=3��OA=4����AD=BD�����ɡ�BDA=90�㣬��BAD=��ABD=45�㣬����MC��x��ɵó���PNF=��ANC=45�㣬��PF��MC��֪��FPN=��PNF=45�㣬��NF=PF=t���ٸ��ݡ�DFM=��ECM=90���֪PF��EC�����ԡ�MPF=��MEC������ME��OB�ó���MEC=��BOD���ʡ�MPF=��BOD��tan��BOD=tan��MPF������MF=3PF=3t������MN=MF+FN���ɵó����ۣ�
��3����OP=m���ı���OMNB�����ΪS��������ON��AM����֤��OAN�ա�ACM��SAS������֪CM=AN=AP����AB=BC=4��CM=AN=AP=4-m��CN=OP=m����M��MF��AC������ΪF����MF=MC•sin60��=$\frac{\sqrt{3}}{2}$��4-m��������S=S��OAC-S��CMN���ɵó����ۣ�
��� �⣺��1����y=-x+4��x�ύ�ڵ�A��
��A��4��0����
�ߵ�B�ĺ�����Ϊ1����ֱ��y=-x+4������B��
��B��1��3����
��������y=ax2+bx����A��4��0����B��1��3����
��$\left\{\begin{array}{l}16a+4b=0\\ a+b=3\end{array}\right.$����ã�$\left\{\begin{array}{l}a=-1\\ b=4\end{array}\right.$��
��a=-1��b=4��
��2����ͼ2����BD��x���ڵ�D���ӳ�MP��x���ڵ�E��
��B��1��3����A��4��0����
��OD=1��BD=3��OA=4��
��AD=3��
��AD=BD��
�ߡ�BDA=90�㣬��BAD=��ABD=45�㣬
��MC��x�ᣬ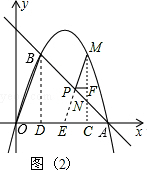
���ANC=��BAD=45�㣬
���PNF=��ANC=45�㣬
��PF��MC��
���FPN=��PNF=45�㣬
��NF=PF=t��
�ߡ�DFM=��ECM=90�㣬
��PF��EC��
���MPF=��MEC��
��ME��OB��
���MEC=��BOD��
���MPF=��BOD��
��tan��BOD=tan��MPF��
��$\frac{BD}{OD}$=$\frac{MF}{PF}$=3��
��MF=3PF=3t��
��MN=MF+FN��
��d=3t+t=4t��
��3���ı���OMNB���������Сֵ��
��OP=m���ı���OMNB�����ΪS��������ON��AM��
�ڡ�OAN���ACM�У�
��$\left\{\begin{array}{l}OA=CA\\��AON=��MAC\\ ON=AM\end{array}\right.$��
���OAN�ա�ACM��SAS����
��CM=AN=AP��
��AB=BC=4��S��ABC=$\frac{\sqrt{3}}{4}$��42=4$\sqrt{3}$��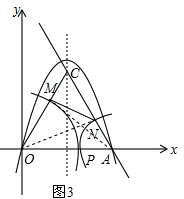
��CM=AN=AP=4-m��CN=OP=m��
��M��MF��AC������ΪF��
��MF=MC•sin60��=$\frac{\sqrt{3}}{2}$��4-m����
��S��CMN=$\frac{1}{2}$CN•MF=$\frac{1}{2}$m•$\frac{\sqrt{3}}{2}$��4-m��=-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m��
��S=S��OAC-S��CMN
=4$\sqrt{3}$-��-$\frac{\sqrt{3}}{4}$m2+$\sqrt{3}$m��
=$\frac{\sqrt{3}}{4}$��m-2��2+3$\sqrt{3}$��
���ڵ�P�˶��Ĺ����У��ı���OMNA���������СֵΪ3$\sqrt{3}$��
���� ���⿼����Ƕ��κ����ۺ��⣬�漰��ȫ�������ε��ж������ʣ������ε���������κ��������ʡ���ת�����ʵ�֪ʶ����2����������ϵʽҪ����������Ǻ���������ʽ����3���������ֵҪת��Ϊ���κ�����ֵ���


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com