
为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
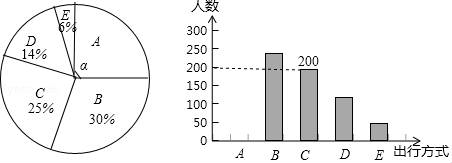
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
科目:初中数学 来源:广东省江门市2017届九年级12月月考数学试卷 题型:填空题
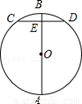
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6, BE=1,则⊙O的直径为________.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:解答题
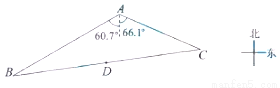
如图,湿地景区岸边有三个观景台 、
、 、
、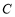 .已知
.已知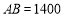 米,
米,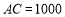 米,
米,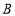 点位于
点位于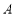 点的南偏西
点的南偏西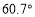 方向,
方向,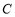 点位于
点位于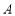 点的南偏东
点的南偏东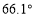 方向.
方向.
(1)求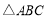 的面积;
的面积;
(2)景区规划在线段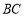 的中点
的中点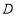 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道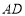 .试求
.试求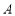 、
、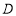 间的距离.(结果精确到
间的距离.(结果精确到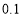 米)
米)
(参考数据: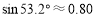 ,
,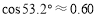 ,
,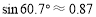 ,
,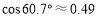 ,
,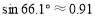 ,
,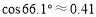 ,
,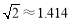 )
)
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
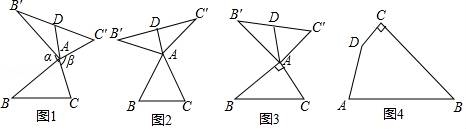
我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2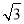 ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
(1)计算: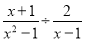 ;
;
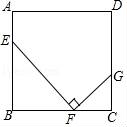
(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(江西卷)数学(解析版) 题型:选择题
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
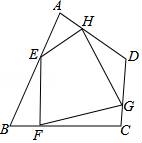
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源:广西钦州市钦南区2016-2017学年第二学期期末考试七年级数学试卷 题型:单选题
下列说法中正确的是( )
A. 旋转一定会改变图形的形状和大小
B. 两条直线被第三条直线所截,同位角相等
C. 在同一平面内,过一点有且只有一条直线与已知直线垂直
D. 相等的角是对顶角
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:选择题
已知圆锥的底面积为9πcm2,母线长为6cm,则圆锥的侧面积是( )
A.18πcm2 B.27πcm2 C.18cm2 D.27cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com