解:(1)由于抛物线y=-x
2-2mx-m
2+2m+1=-(x+m)
2+2m+1,
即顶点坐标(-m,2m+1),
而抛物线的顶点坐标为(-1,3);
故m=1;
(2)由(1)可知抛物线的解析式为y=-(x+1)
2+3,
即y=-x
2-2x+2;
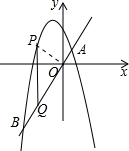
设P(x,-x
2-2x+2),
因为PQ∥y轴,
所以设Q(x,2x),
所以:PQ=(-x
2-2x+2)-2x=-x
2-4x+2=-(x+2)
2+6;
当x=-2时,PQ最大值=6;
(3)因为∠PQO不可能为直角,
所以分两种情形讨论:
①当∠QPO为直角时,P为抛物线与x轴的左侧的交点;
抛物线:y=-x
2-2x+2,令y=0-x
2-2x+2=0,
解得:x
1=-1+

,x
2=-1-

;
所以P(-1-

,0);
当x=-1-

时,y=2x=2(-1-

)=-2-2

,
所以Q(-1-

,-2-2

);
②当∠POQ为直角时,设PQ与x轴交于D点;
根据题意:△OPD∽△OQD,
得:OD
2=PD•QD;
即x
2=(-x
2-2x+2)(-2x),
解得x=
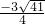
,
取x<0,则x=
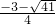
;
当x=
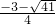
时,y=2x=
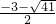
,
所以Q(
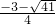
,
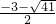
);
所以,符合条件的Q坐标为(-1-

,-2-2

)或(
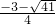
,
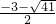
).
分析:(1)将抛物线的解析式化为顶点坐标式,然后用m表示出抛物线的顶点坐标,即可求得m的值;
(2)设出点P的横坐标,根据抛物线和直线y=2x的解析式可表示出P、Q的纵坐标,进而可得到关于PQ的长和P点横坐标的函数关系式,根据函数的性质即可求得PQ的最大值;
(3)显然∠PQO<90°,那么可分两种情况考虑:
①∠OPQ=90°,此时P为抛物线与x轴的交点,根据抛物线的解析式,即可求得点P坐标,将点P的横坐标代入直线y=2x中,即可求得点Q的坐标;
②∠POQ=90°,若设PQ与x轴的交点为D,在Rt△OPQ中,OD⊥PQ,根据射影定理得OD
2=DP•DQ,由此可得到关于P点横坐标(即Q点横坐标)的方程,从而求得Q点横坐标,将其代入直线y=2x中,即可求得Q点坐标.
点评:此题主要考查了二次函数解析式的确定、二次函数最值的应用、直角三角形的判定等知识;(3)题中,由于直角三角形的直角顶点不确定,一定要分类讨论,以免漏解.

 已知抛物线y=-x2-2mx-m2+2m+1的顶点坐标为(-1,3),
已知抛物线y=-x2-2mx-m2+2m+1的顶点坐标为(-1,3),
 ,x2=-1-
,x2=-1- ;
; ,0);
,0); 时,y=2x=2(-1-
时,y=2x=2(-1- )=-2-2
)=-2-2 ,
, ,-2-2
,-2-2 );
);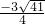 ,
,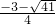 ;
;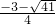 时,y=2x=
时,y=2x=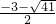 ,
,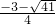 ,
,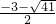 );
); ,-2-2
,-2-2 )或(
)或(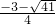 ,
,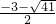 ).
).

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.