解:(1)∵抛物线y=ax
2+bx+3经过点A(-1,0),B(3,0)
∴

,
解得:
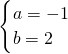
,
∴y=-x
2+2x+3;
∴y=-(x-1)
2+4,
∴M(1,4).
(2)设点P的坐标为(0,y),
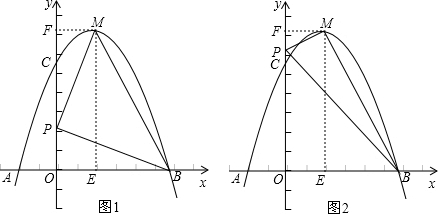
①若∠MPB=90°,如图1,过点M作ME⊥x轴,MF⊥y轴,
∴∠MFP=∠BOP=90°.
∵∠MPB=90°,
∴∠MPF=∠PBO,
∴Rt△PFM∽Rt△BOP,
∴
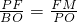
.
∴
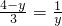
,
解得:y
1=1,y
2=3
∴点P的坐标为(0,1),(0,3);
②若∠PMB=90°,如图2,过点M作ME⊥x轴,MF⊥y轴,
同理,Rt△PFM∽Rt△BEM,
∴
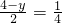
,
解得:y=

∴点P的坐标为 (0,

)
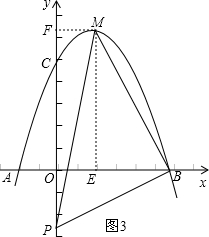
③若∠MBP=90,如图3,过点M作ME⊥x轴,MF⊥y轴,
同理,Rt△POB∽Rt△BEM,
∴
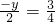
,
解得:y=-

,
∴点P的坐标为 (0,-

).
综上:△PBM是直角三角形时,P点的坐标为(0,1),(0,3),(0,

),(0,-

).
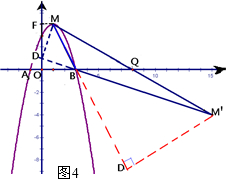
(3)由题意可知:B(3,0),M(1,4),Q(8,0),点M,M′关于点Q中心对称,
∴M′(15,-4),
连结M′B,并延长M′B交y轴于点D,
由y
M′D=-

+1,
∴D(0,1).
连结MD,
∵在Rt△DFM和Rt△DOB中
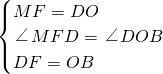
∴Rt△DFM≌Rt△DOB(SAS),
∴MD=BD.
∴△DBM是等腰直角三角形,
∴∠DBM=45°,
∴∠MBM′=135°.
分析:(1)直接运用待定系数法求出a、b的值就可以求出结论;
(2)设点P的坐标为(0,y),分三种情况进行讨论,若∠MPB=90°,如图1,过点M作ME⊥x轴,MF⊥y轴,通过证明Rt△PFM∽Rt△BOP,由相似三角形的性质就可以求出结论,∠PMB=90°,如图2,过点M作ME⊥x轴,MF⊥y轴,若∠MBP=90,如图3,过点M作ME⊥x轴,MF⊥y轴,类似的方法证明三角形相似就可以求出点P的坐标;
(3)由旋转可以求出M′的坐标,连结M′B,并延长M′B交y轴于点D,求出M′D的解析式,求出D的坐标,通过得出Rt△DFM≌Rt△DOB就可以而出MD=BD.进而△DBM是等腰直角三角形,从而可以得出结论.
点评:本题考查了待定系数法求函数的解析式的运用,直角三角形的性质的运用,相似三角形的判定及性质的运用,全等三角形的判定及性质的运用,旋转的性质的运用,等腰直角三角形的性质的运用,解答本题时运用函数的性质解答是关键.

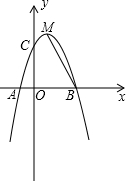 已知抛物线y=ax2+bx+3经过点A(-1,0),B(3,0),交y轴于点C,M为抛物线的顶点,连接MB.
已知抛物线y=ax2+bx+3经过点A(-1,0),B(3,0),交y轴于点C,M为抛物线的顶点,连接MB.
 ,
,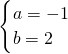 ,
,
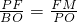 .
.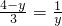 ,
,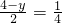 ,
,
 )
)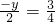 ,
, ,
, ).
).
 ),(0,-
),(0,- ).
). +1,
+1,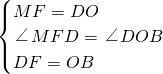


 阅读快车系列答案
阅读快车系列答案 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=