解:(1)由题意可得:

,
解得
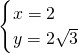
,
所以点P的坐标为(2,2

);
(2)将y=0代入y=-

x+4

,-

x+4

=0,
∴x=4,即OA=4,
作PD⊥OA于D,则OD=2,PD=2

,
∵tan∠POA=
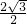
=

,
∴∠POA=60°,
∵OP=
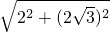
=4,
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,

∵∠EOF=60°,OE=t,
∴EF=
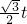
,OF=

,
∴S=

•OF•EF=

t
2.
当4<t<8时,如图,设EB与OP相交于点C,
∵CE=PE=t-4,AE=8-t,
∴AF=4-

,EF=

(8-t),
∴OF=OA-AF=4-(4-

)=

,
∴S=

(CE+OF)•EF=

(t-4+

t)×

(8-t),
=-


t
2+4

t-8

;
②当0<t≤4时,S=

,t=4时,S
最大=2

;

当4<t<8时,S=-


t
2+4

t-8

=-


(t-

)
2+


,
t=

时,S
最大=


.
∵


>2

,
∴当t=

时,S最大,最大值为


.
分析:(1)由两直线相交可列出方程组,求出P点坐标;
(2)将y=0代入y=-

x+4

,可求出OA=4,作PD⊥OA于D,则OD=2,PD=2

,利用tan∠POA=

,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
(3)①当0<t≤4时,在Rt△EOF中,∠EOF=60°,OE=t,则EF=
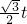
,OF=

,则S=

•OF•EF=

t
2;
②当4<t<8时,如图,设EB与OP相交于点C,易知:CE=PE=t-4,AE=8-t,可得AF=4-

,EF=

(8-t),有OF=OA-AF=4-(4-

)=

,S=

(CE+OF)•EF=-


t
2+4

t-8

.
点评:把动点问题与三角形的性质相结合,增加了难度,在解答时要注意t在三个取值范围内的情况,不要漏解.

 已知:如图,直线y=-
已知:如图,直线y=- x+4
x+4 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y= x相交于点P.
x相交于点P. ,
,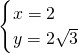 ,
, );
); x+4
x+4 ,-
,- x+4
x+4 =0,
=0, ,
,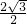 =
= ,
,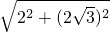 =4,
=4, ∵∠EOF=60°,OE=t,
∵∠EOF=60°,OE=t,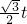 ,OF=
,OF= ,
, •OF•EF=
•OF•EF= t2.
t2. ,EF=
,EF= (8-t),
(8-t), )=
)= ,
, (CE+OF)•EF=
(CE+OF)•EF= (t-4+
(t-4+ t)×
t)× (8-t),
(8-t),
 t2+4
t2+4 t-8
t-8 ;
; ,t=4时,S最大=2
,t=4时,S最大=2 ;
;

 t2+4
t2+4 t-8
t-8 =-
=-
 (t-
(t- )2+
)2+
 ,
, 时,S最大=
时,S最大=
 .
.
 >2
>2 ,
, 时,S最大,最大值为
时,S最大,最大值为
 .
. x+4
x+4 ,可求出OA=4,作PD⊥OA于D,则OD=2,PD=2
,可求出OA=4,作PD⊥OA于D,则OD=2,PD=2 ,利用tan∠POA=
,利用tan∠POA= ,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
,可知∠POA=60°,由OP=4.可知△POA是等边三角形;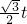 ,OF=
,OF= ,则S=
,则S= •OF•EF=
•OF•EF= t2;
t2; ,EF=
,EF= (8-t),有OF=OA-AF=4-(4-
(8-t),有OF=OA-AF=4-(4- )=
)= ,S=
,S= (CE+OF)•EF=-
(CE+OF)•EF=-
 t2+4
t2+4 t-8
t-8 .
.

 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=