
�п���������ǰ��ij��������Ϊ���˽�ѡ���������ϵij��������ijɼ�������������˱�������ѡ������������Ŀ�ij��������ijɼ����������Եõ��ijɼ����������������������ͳ��ͼ��
�������ͼ�е���Ϣ������������⣺
��
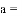
��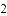
��
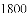
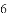
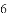
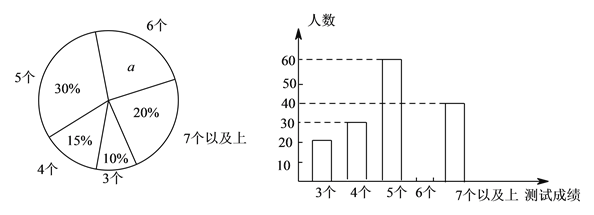
 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���Ϻ����ֶ��������Ľ�����2018����꼶�п���ѧģ���Ծ���3�·ݣ� ���ͣ������
�ⷽ��x2+x+1=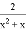 ʱ�������y=x2+x����ôԭ���̿ɻ�Ϊ_____��
ʱ�������y=x2+x����ôԭ���̿ɻ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶�п�ģ����ѧ�Ծ� ���ͣ������
ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ�͡�ѧ���������Ȥ���á������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��
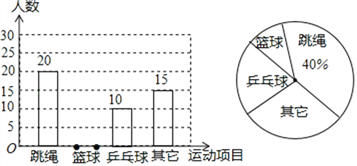
��1������ε����У�ϲ��������Ŀ��ͬѧ�ж����ˣ�
��2��������ͳ��ͼ�У���ƹ���İٷֱ�Ϊ���٣�
��3�����ѧУ��800��ѧ��������ȫУѧ�����ж�����ϲ��������Ŀ��
��4���뽫����ͳ��ͼ����������
��5���ڱ������ѧ���У�ϲ���������2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ�����༶�μ�У����ӣ��������б�����״ͼ�������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶�п�ģ����ѧ�Ծ� ���ͣ���ѡ��
��֪a��b��c�ǡ�ABC�����߳����ҷ���a��1+x2��+2bx��c��1��x2��=0��������ȣ����ABCΪ��������
A. ���������� B. ֱ�������� C. �ȱ������� D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��һ��ģ�⿼����ѧ�Ծ� ���ͣ������
��ͼ����ABC�У�AB=AC����DΪBC��һ�㣬��AD=DC����A��B��D��������O��AE�ǡ�O��ֱ��������DE��
��1����֤��AC�ǡ�O�����ߣ�
��2����sinC= ��AC=6�����O��ֱ����
��AC=6�����O��ֱ����
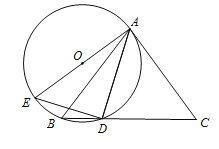
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��һ��ģ�⿼����ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABCD�У�E��F�ǶԽ���BD�ϵ����㣬Ҫʹ�ı���AFCE��ƽ���ı��Σ��������ӵ�һ������������_____����ֻ����һ��������
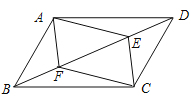
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��һ��ģ�⿼����ѧ�Ծ� ���ͣ������
�ҹ��Ϻ���Դ�ḻ�������ԼΪ3 500 000ƽ��ǧ�ף��൱���ҹ��������ƺ��Ͷ����������3��������3 500 000�ÿ�ѧ��������ʾΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ���®����2018����꼶�п�һģ��ѧ�Ծ� ���ͣ������
����ֽƬABCD�У���֪AD=8��AB=6��E�DZ�BC�ϵĵ㣬��AEΪ�ۺ��۵�ֽƬ��ʹ��B���ڵ�F��������FC������EFCΪֱ��������ʱ��BE�ij�Ϊ�� ����
���𰸡�3��6
�����������������
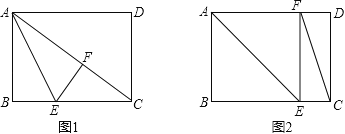
�������֪�������������ͼ1��ͼ2��
ͼ1������F�ڶԽ���AC��ʱ����EFC=90�㣬
�ߡ�AFE=��B=90�㣬��EFC=90�㣬
���A��F��C���ߣ�
�߾���ABCD�ı�AD=8��
��BC=AD=8��
��Rt��ABC��AC=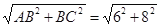 =10��
=10��
��BE=x����CE=BC��BE=8��x��
�ɷ��۵����ʵã�AF=AB=6��EF=BE=x��
��CF=AC��AF=10��6=4��
��Rt��CEF��EF2+CF2=CE2��
��x2+42=��8��x��2��
���x=3��
��BE=3��
ͼ2������F����AD����ʱ����CEF=90�㣬
�ɷ��۵����ʵã���AEB=��AEF=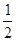 ��90��=45�㣬
��90��=45�㣬
���ı���ABEF�������Σ�
��BE=AB=6��
����������BE�ij�Ϊ3��6��
�ʴ�Ϊ��3��6��
���㣺1����Գƣ����۱任����2�����ɶ���
�����͡������
��������
15
���㣺( )��2��
)��2��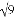 +��
+��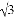 ��4��0��
��4��0��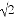 cos45�㣮
cos45�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��18�� ƽ���ı��� ��Ԫ���� ���ͣ���ѡ��
��ͼ����ƽ���ı���ABCD�ĶԽ���BD��һ��M�ֱ���ƽ���ı������ߵ�ƽ����EF��GH����ôͼ�е�ƽ���ı���AEMG�����S1��ƽ���ı���HCFM�����S2�Ĵ�С��ϵ�ǣ� ��
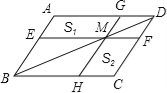
A. S1��S2 B. S1=S2 C. S1��S2 D. 2S1=S2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com