




 。
。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
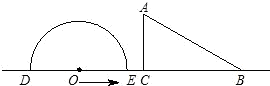
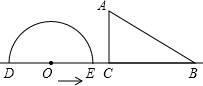 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?查看答案和解析>>
科目:初中数学 来源:2005年初中毕业升学考试(江苏南京卷)数学(带解析) 题型:解答题
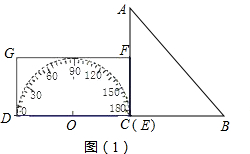
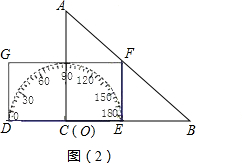
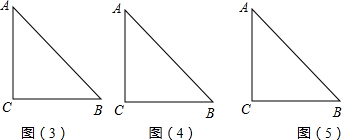
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=
30°,BC=12cm.半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t (s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.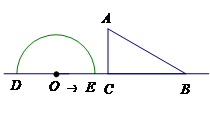
(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源:2005年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=
30°,BC=12cm.半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t (s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
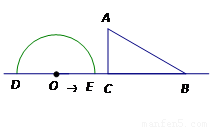
(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com