解:(1)∵AC=BC=4,
∴AB=

=
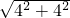
=4

,
∵M是AB的中点,
∴CM⊥AB,AM=CM=

AB=

×4

=2

,
∴阴影部分的面积=

AM•CM=

×2

×2

=4,
周长=AB+AM+CM=4+2

+2

=4+4

;
(2)设MN与AC的交点为D,BC与MK的交点为G,
∵旋转角是45°,
∴∠AMD=45°,

又∵△ABC是等腰直角三角形,
∴∠B=45°,
∴∠AMD=∠B=45°,
∴DM∥BC,
∵M是AB的中点,
∴DM是△ABC的中位线,
∴DM=

BC=

×4=2,
同理可得,MG=

AC=

×4=2,
∴四边形DCGM是正方形,
∴阴影部分的面积=2
2=4,
周长=2×4=8;
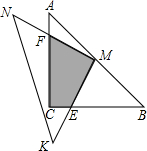
(3)如图,过点M作ME⊥AC于E,作MF⊥BC于F,
∵M是等腰直角△ABC斜边AB的中点,
∴四边形ECMF是正方形,
∴ME=MF,
∵∠DME+∠EMG=∠NMK=90°,
∠GMF+∠EMG=∠EMF=90°,
∴∠DME=∠GMF,
在△DME和△GMF中,

,
∴△DME≌△GMF(ASA),
∴S
△DME=S
△GMF,
∴阴影部分的面积=正方形ECMF的面积,
∵M是AB的中点,
∴ME是△ABC的中位线,
∴ME=

BC=

×4=2,
∴正方形ECMF的面积=2
2=4,
∴阴影部分的面积=4.
故答案为:(1)4,4+4

;(2)4,8;(3)4.
分析:(1)利用勾股定理列式求出AB,再根据等腰直角三角形的性质可得CM⊥AB,AM=CM=

AB,然后求解即可;
(2)设MN与AC的交点为D,BC与MK的交点为G,根据旋转角是45°求出∠AMD=45°,然后根据同位角相等,两直线平行求出DM∥BC,从而判定DM是△ABC的中位线,然后求出DM=

BC,同理求出MG=

AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积与周长即可;
(3)过点M作ME⊥AC于E,作MF⊥BC于F,可得四边形ECMF是正方形,根据正方形的性质可得ME=MF,再根据同角的余角相等求出∠DME=∠GMF,然后利用“角边角”证明△DME和△GMF全等,根据全等三角形面积相等可得△DME和△GMF的面积相等,然后求出阴影部分的面积等于正方形ECMF的面积,根据三角形的中位线平行于第三边并且等于第三边的一半求出ME,然后求解即可.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,以及正方形的判定与性质,(3)作辅助线构造出全等三角形与正方形并求出阴影部分的面积等于正方形的面积是解题的关键.


 =
=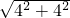 =4
=4 ,
, AB=
AB= ×4
×4 =2
=2 ,
, AM•CM=
AM•CM= ×2
×2 ×2
×2 =4,
=4, +2
+2 =4+4
=4+4 ;
;
 BC=
BC= ×4=2,
×4=2, AC=
AC= ×4=2,
×4=2, ,
, BC=
BC= ×4=2,
×4=2, ;(2)4,8;(3)4.
;(2)4,8;(3)4. AB,然后求解即可;
AB,然后求解即可; BC,同理求出MG=
BC,同理求出MG= AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积与周长即可;
AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积与周长即可;

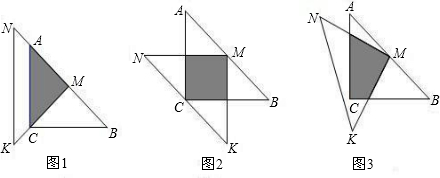
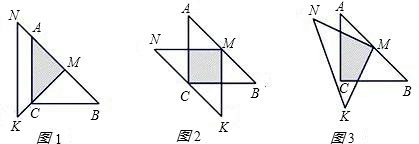
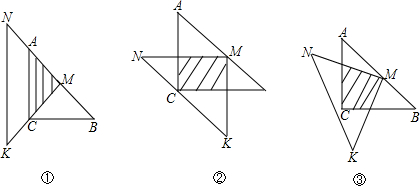
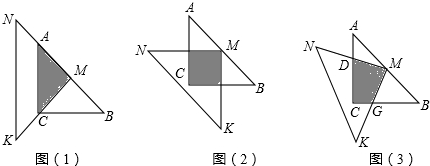
 如图所示,一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动;将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
如图所示,一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动;将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.