已知三角形两边的长分别是6和12.则此三角形第三边的长可能是( )A．5B．6C．11D．18 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

9．已知三角形两边的长分别是6和12，则此三角形第三边的长可能是（　　）

A．

B．

C．

D．

分析已知三角形的两边长分别为6和12，根据在三角形中任意两边之和＞第三边，任意两边之差＜第三边；即可求第三边长的范围．

解答解：设第三边长为x，则由三角形三边关系定理得12-6＜x＜12+6，即6＜x＜18．
因此，本题的第三边应满足6＜x＜18，把各项代入不等式符合的即为答案．
只有11符合不等式，
故选C．

点评此题考查了三角形的三边关系，是求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

19．计算
（1）$\sqrt{（-4）^{2}}$+$\root{3}{（-4）^{3}}$×（-$\frac{1}{2}$）²=
（2）$\frac{2x-6}{x-2}$÷$\frac{{x}^{2}-9}{x-2}$+1=

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．

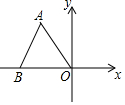等边△ABO在平面直角坐标系内的位置如图所示，已知△ABO的边长为6，则点A的坐标为（　　）

A．

（-3，3）

B．

（3，-3$\sqrt{3}$）

C．

（-3，3$\sqrt{3}$）

D．

（-3，-3$\sqrt{3}$）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

17．下列各组整式中，不是同类项的是（　　）

A．

3x³y与xy³

B．

-2016与2017

C．

4ab²与-3ab²

D．

2ab与10²⁰ab

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．

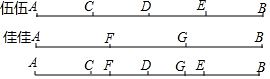在学习了线段的相关知识后，伍伍与佳佳对一根细绳AB进行了如下研究：伍伍把细绳AB折叠，找到了它的三个四等分点，分别为C、D、E；佳佳再把细绳AB进行折叠，找到了它的两个三等分点，分别为F、G，如图所示，伍伍度量出CF=5厘米，求细绳AB的长度．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．某工厂现在平均每天比原计划多生产10台机器，现在生产700台机器所需时间与原计划生产500台机器所需时间相同，设原计划平均每天生产x台机器，根据题意列方程得（　　）

A．

$\frac{700}{x}$=$\frac{500}{x+10}$

B．

$\frac{700}{x-10}$=$\frac{500}{x}$

C．

$\frac{700}{x}$=$\frac{500}{x-10}$

D．

$\frac{700}{x+10}$=$\frac{500}{x}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．观察下列运算：
①由（$\sqrt{2}$+1）（$\sqrt{2}$-1）=1，得$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1；
②由（$\sqrt{3}$+$\sqrt{2}$）（$\sqrt{3}$-$\sqrt{2}$）=1，得$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}-\sqrt{2}$；
③由（$\sqrt{4}$+$\sqrt{3}$）（$\sqrt{4}$-$\sqrt{3}$）=1，得$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\sqrt{4}$-$\sqrt{3}$；
…
（1）通过观察你得出什么规律？用含n的式子表示出来；
（2）利用（1）中你发现的规律计算：（$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2016}}$）×（$\sqrt{2017}$+1）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．学校举行广播操比赛，八年级三个班的各项得分及三项得分的平均数如下（单位：分）．