练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若AD=BC,∠A=∠B,直接能利用“SAS”证明△ADF≌△BCE的条件是( )

    A. AE=BF B. DF=CE C. AF=BE D. ∠CEB=∠DFA

    C 【解析】试题分析：用边角边证明两三角形全等，已知其中一个对应角相等和一条对应边相等，则还需要的条件是相等角的另外一条临边相等，即AF=BE，故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

    一个矩形和一个平行四边形的边分别相等， 若矩形面积为这个平行四边形的面积的2倍，则平行四边形的锐角的度数为（ ）．

    A. 15° B. 30° C. 45° D. 60°

    B 【解析】如图，矩形ABCD与平行四边形BCFG中，BG=AB， 过点G作GH⊥BC，垂足为H， ∵S矩形ABCD=BC·AB=2S平行四边形BCFG=2BC·GH，∴BG=2GH， ∵△BGH是Rt△，∠BHG=90°，∴∠GBH=30°， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 25.1.1随机事件 测试 题型：解答题

    如图所示,第一行表示各盒中球的颜色、个数情况,第二行表示摸到红球的可能性大小,请你用线把它们连接起来.

    连线见解析 【解析】试题分析：结合各个盒子里红球、白球的个数，根据红球的个数越多，则被摸到的可能性越大，即可解决问题. 试题解析：如图所示：

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）练习 题型：填空题

    如图，PA、PB分别切圆O于A、B两点，并与圆O的切线分别相交于C、D两点，已知PA=7cm，则△PCD的周长等于_________．

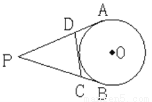
    14. 【解析】 试题分析：由于DA、DC、BC都是⊙O的切线，可根据切线长定理，将△PCD的周长转换为PA、PB的长，然后再进行求解． 试题解析：如图，设DC与⊙O的切点为E； ∵PA、PB分别是⊙O的切线，且切点为A、B； ∴PA=PB=7cm； 同理，可得：DE=DA，CE=CB； 则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=P...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型：填空题

    如图,∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是_______.

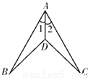
    ∠B=∠C 【解析】本题要判定△ABD≌△ACD，已知∠1=∠2，AD是公共边，具备了一边一角对应相等，注意“AAS”的条件；两角和其中一角的对应边相等，只能选∠B=∠C. 【解析】 由图可知，只能是∠B=∠C，才能组成“AAS”. 故填∠B=∠C.

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册13.4课题学习 最短路径问题同步练习题 题型：解答题

    公园内两条小河MO，NO在O处汇合，两河形成的半岛上有一处景点P(如图所示)．现计划在两条小河上各建一座小桥Q和R，并在半岛上修三段小路，连通两座小桥与景点，这两座小桥应建在何处才能使修路费用最少？请说明理由．

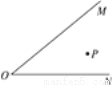
    见解析 【解析】试题分析：可过点P分别作关于OM，ON的对称点P′，P″，连接P′P″，与OM、ON的交点即为满足条件的建桥地点. 试题解析：如图，作P关于OM的对称点P′，作P关于ON的对称点P″，连接P′P″，分别交MO，NO于Q，R，连接PQ，PR，则P′Q＝PQ，PR＝P″R，则Q，R就是小桥所在的位置． 理由：在OM上任取一个异于Q的点Q′，在ON上任取一个异于R的点R...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．

    求证：（1）FC＝AD；

    （2）AB＝BC＋AD．

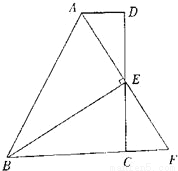
    （1）证明见解析；（2）证明见解析. 【解析】试题分析:（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答． （2）根据线段垂直平分线的性质判断出AB=BF即可． 证明：（1）∵AD∥BC（已知）， ∴∠ADC=∠ECF（两直线平行，内错角相等）， ∵E是CD的中点（已知）， ∴DE=EC（中点...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图，直线CP是AB的中垂线且交AB于P，其中AP＝2CP．甲、乙两人想在AB上取两点D、E，使得AD＝DC＝CE＝EB，其作法如下：

    甲：作∠ACP、∠BCP之角平分线，分别交AB于D、E，则D、E即为所求；

    乙：作AC、BC之中垂线，分别交AB于D、E，则D、E即为所求．

    对于甲、乙两人的作法，下列判断何者正确（　　）

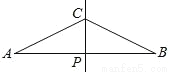
    A. 两人都正确 B. 两人都错误 C. 甲正确，乙错误 D. 甲错误，乙正确

    D 【解析】试题解析： 甲、乙都正确， 理由是：∵CP是线段AB的垂直平分线， ∴BC=AC，∠APC=∠BPC=90°， ∵AC=2CP， ∴∠A=30°， ∴∠ACP=60°， ∵CD平分∠ACP， ∴∠ACD=∠ACP=30°， ∴∠ACD=∠A， ∴AD=DC， 同理CE=BE， 即D、E为所求； ∵D在A...

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：单选题

    一次函数y1=kx+b与y2=x+a的图象如图，则下列结论①k＜0；②a＞0；③当x＜3时，y1＜y2中，正确的个数是（　　）

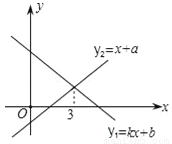
    A. 0 B. 1 C. 2 D. 3

    B 【解析】试题分析：∵y1=kx+b的函数值随x的增大而减小，∴k＜0；故①正确 ∵y2=x+a的图象与y轴交于负半轴，∴a＜0； 当x＜3时，相应的x的值，y1图象均高于y2的图象， ∴y1＞y2，故②③错误．

    查看答案和解析>>

    同步练习册答案