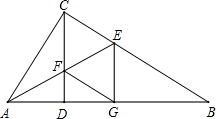
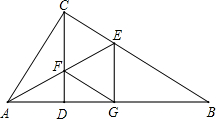
(1)四边形CEGF为菱形.
证明:∵AF平分∠CAB,
∴∠CAF=∠GAF,
∵FG∥BC,
∴∠B=∠AGF,
∵∠ACD=∠B,
∴∠ACF=∠AGF,
∴在△AFC和△AFG中,
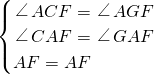
,
∴△AFC≌△AFG(AAS),
∴CF=GF,∠CFA=∠GFA,
∴∠CFE=∠GFE,
∵在△CFE和△GFE中,
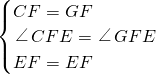
,
∴△CFE≌△GFE(SAS),
∴∠FCE=∠FGE,∠CFE=∠GFE,∠CEF=∠GEF,
∴∠CFG=∠CEG,
∴四边形CFGE为平行四边形,
∵CF=FG,
∴四边形CEGF为菱形.
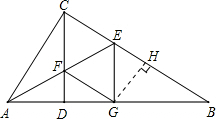
(2)解:作GH⊥BC于点H,
∴S
△GEB=BE•GH•

,S
菱形CFGE=CE•GH,
∵△ABC∽△GEB,且相似比为2:1,
∴BE:AB=1:2,
∴S
△ABC:S
△GEB=4:1,
∴S
△ABC=4S
△GEB=4•BE•GH•

=2BE•GH,
设BE=a,CE=EG=b,则a>b,
∵△ABC和△GEB相似,且相似比是2:1,
∴

=
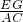
=
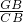
=

,
∴AB=2a,AC=2b=AG,BC=BE+EC=a+b,
∴BG=2a-2b,
∴

=

∴5b-3a=0,即a=

b,即BE=

b,
∴
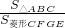
=
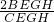
=
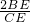
=
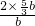
=

∴△ABC和四边形CEGF的面积的比为10:3.
分析:(1)通过求证△AFC和△AFG,推出∠CFE=∠GFE,CF=GF,再通过求证△CFE≌△GFE,推出∠FCE=∠FGE,∠CFG=∠CEG,依据平行四边形的判定定理即可得四边形CFGE为平行四边形,由CF=FG,即可推出四边形CEGF为菱形.
(2)作GH⊥BC于点H,即可推出S
△GEB和S
菱形CFGE,再通过△ABC和△GEB的相似比推出其面积比,CE:GB=1:2,即可得S
△ABC=4S
△GEB=4•BE•GH•

=2BE•GH,然后,即可推出△ABC和菱形CEGF的面积的比为10:3.
点评:本题主要考查全等三角形的判定与性质、相似三角形的性质、菱形的判定定理、平行的相关性质等知识点,关键在于熟练正确地运用各性质定理,正确地作出辅助线,认真的表示出有关图形的面积.

 BC交AB于点G,连接EG.
BC交AB于点G,连接EG.
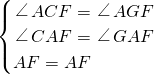 ,
,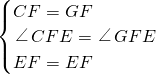 ,
,
 ,S菱形CFGE=CE•GH,
,S菱形CFGE=CE•GH, =2BE•GH,
=2BE•GH, =
=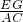 =
=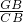 =
= ,
, =
=
 b,即BE=
b,即BE= b,
b,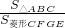 =
=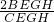 =
=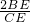 =
=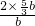 =
=
 =2BE•GH,然后,即可推出△ABC和菱形CEGF的面积的比为10:3.
=2BE•GH,然后,即可推出△ABC和菱形CEGF的面积的比为10:3.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是
16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是