
 如图:A、B两点与建筑物底部D在一直线上,从建筑物顶部C点测得A、B两点的俯角分别是30°、60°,且AB=20,求建筑物CD的高.
如图:A、B两点与建筑物底部D在一直线上,从建筑物顶部C点测得A、B两点的俯角分别是30°、60°,且AB=20,求建筑物CD的高.科目:初中数学 来源: 题型:
 15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:
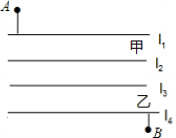 如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.图中的尺寸是:甲河宽8米,乙河宽10米,A到甲河垂直距离为40米,B到乙河垂直距离为20米,两河距离100米,A、B两点水平距离(与小河平行方向)120米,为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、D两点间来往的路程是多少米?
如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,l1∥l2表示小河甲,l3∥l4表示小河乙,A为校本部大门,B为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.图中的尺寸是:甲河宽8米,乙河宽10米,A到甲河垂直距离为40米,B到乙河垂直距离为20米,两河距离100米,A、B两点水平距离(与小河平行方向)120米,为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、D两点间来往的路程是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
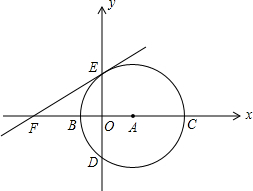 于B、C两点,与y轴相交于D、E两点.
于B、C两点,与y轴相交于D、E两点.| 1 |
| 4 |
| 16 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•建邺区一模)如图,在直角坐标系中,直线y=2x与双曲线y=
(2013•建邺区一模)如图,在直角坐标系中,直线y=2x与双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
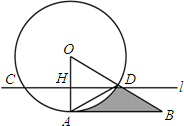 (2013•建邺区一模)如图,直线l与⊙O交于C、D两点,且与半径OA垂直,垂足为H,∠ODC=30°,在OD的延长线上取一点B,使得AD=BD.
(2013•建邺区一模)如图,直线l与⊙O交于C、D两点,且与半径OA垂直,垂足为H,∠ODC=30°,在OD的延长线上取一点B,使得AD=BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com