
分析 先化简,再计算即可.
解答 解:∵$\frac{x}{y+z}$=a,$\frac{y}{z+x}$=b,$\frac{z}{x+y}$=c,
∴$\frac{1}{a}$=$\frac{y+z}{x}$,$\frac{1}{b}$=$\frac{x+z}{y}$,$\frac{1}{c}$=$\frac{x+y}{z}$,
原式=$\frac{1}{\frac{1+a}{a}}$+$\frac{1}{\frac{1+b}{b}}$+$\frac{1}{\frac{1+c}{c}}$
=$\frac{1}{1+\frac{1}{a}}$+$\frac{1}{1+\frac{1}{b}}$+$\frac{1}{1+\frac{1}{c}}$
=$\frac{1}{1+\frac{y+z}{x}}$+$\frac{1}{1+\frac{x+z}{y}}$+$\frac{1}{1+\frac{x+y}{z}}$
=$\frac{1}{\frac{x+y+z}{x}}$+$\frac{1}{\frac{x+y+z}{y}}$+$\frac{1}{\frac{x+y+z}{z}}$
=$\frac{x}{x+y+z}$+$\frac{y}{x+y+z}$+$\frac{z}{x+y+z}$
=$\frac{x+y+z}{x+y+z}$
=1,
故答案为1.
点评 本题考查了比例的性质,以及分式的加减,掌握分式加减的法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
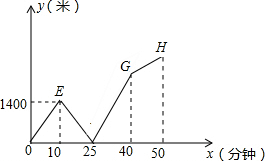 如图,小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中.如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图.则小明的家和小亮的家相距2975米.
如图,小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中.如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图.则小明的家和小亮的家相距2975米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
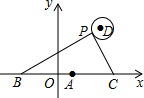 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,4cm,8cm | B. | 17cm,7cm,9cm | C. | 12cm,14cm,20cm | D. | 5cm,5cm,11cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com