练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，作90°角的步骤：(1)画直线________；(2)以l上任一点为圆心，________长为半径画弧交l于点________；(3)以A、B为圆心，________长为半径画弧，两弧相交于________；(4)连结OC，则OC⊥AB，即∠COB＝90°．

    答案：
    解析：

    (1)1　(2)任意长　A　B　(3)大于AB　C点


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （1）如图1，请你将一张长方形的纸对折、再对折，然后按图中所示随意撕去一小部分，再将纸展开，把得到的图案画在试卷上，从对称的角度来说，你画出的这个图形有哪些几何特征？
    （2）如图2，已知△ABC．
    ①作∠B的角平分线；（要求：用尺规作图、保留作图痕迹，不写作法和证明）
    ②若∠C=90°，∠B=60°，BC=4，∠B的平分线交AC于D，请求出线段BD的长．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    平面上的点M关于直线l有唯一的轴对称点M′，这样平面上的任意一点就与该点关于这条直线的轴对称点之间建立了一种对应关系，我们把这种对应关系叫做点M关于直线l的轴对称变换，记为M
    M(l)
    M′(l)    ，点M的轴对称点就记为M′（l），如图（1）所示．如果先作平面上的点M关于直线l的轴对称变换M
    M(l)
    M′(l)    ，得到对应点M′（l），然后，再作M′（l）关于另外一条直线m的轴对称变换M′(l)
    M(m)
    Mn(l，m)    ，这样点M就与该点关于直线l和m的轴对称点M′′（l，m）之间建立了一种对应关系，我们把这种对应关系就叫做点M关于直线l和m的轴对称变换，记为M′(l)
    M(m)
    Mn(l，m)    ，M的对应点就记为M′′（l，m）．如图（2），M是平面上的一点，直线l、m相交所成的角为θ（0°＜θ≤90°），且交点为O，请回答如下问题：
    （1）在图（2）中，求作M′（l）和M′′（l，m）．（要求保留作图痕迹）
    （2）当θ=
     
    °时，M与M′′（l，m）关于点O成中心对称．
    （A）30（B）45（C）60（D）90
    （3）（在以下两题中任选一题作答）
    ①试探讨∠MOM′′（l，m）与θ之间的数量关系，并证明你的结论．
    ②试探讨OM与OM′′（l，m）间的数量关系，并证明你的结论．
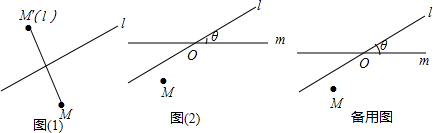
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2014沪科版七年级上册(专题训练　状元笔记)数学：第四章　直线与角 沪科版 题型：044

    (1)探索

    上面三个图中∠AOB是平角，OE，OD分别是∠COB和∠COA的平分线．

    在图1中，∠BOC＝60度，通过计算，∠DOE的度数为(　　)度；

    在图2中，∠BOC＝90度，通过计算，∠DOE的度数为(　　)度；

    在图3中，∠BOC＝130度，通过计算，∠DOE的度数为(　　)度；

    (2)发现像上面这样过平角的顶点引一条射线将其分成相邻的两个角，然后做这两个角的平分线，这两条角平分线所成的角为(　　)度．

    (3)应用

    一次木工师傅急着要用一个直角拐尺，即直角三角板，来画一个直角，但是忘记带了，于是他寻找了一张不规则的纸片，但是有一条边FG恰好是直线，并且将这张纸片作了如图所示的操作，将纸片折叠成∠ADE，然后根据这个简易模型画了一个角，他这样做可行吗？请你说出其中的道理．

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：059

    如下图所示，∠APC称为圆内角(角的顶点在圆内且与圆心不重合)．

    (1)请同学们按以下步骤作图：

    ①用圆规作⊙O；

    ②在⊙O内作一个圆内角∠APC(∠APC≤90°)；

    ③延长AP，CP交⊙O于B，D两点；

    ④连接OA，OB，OC，OD．

    (2)按此作图步骤再重复作一个图形，对应点用，，，，，来表示．

    (3)用量角器量出两图中的下列各角的度数：∠APC＝________，∠＝________，∠AOC＝________，∠＝________，∠BOD＝________，∠＝________．

    (4)根据上面量得的两组数据猜想∠APC与∠AOC，∠BOD有什么数量关系？

    (5)根据你所作的(1)中的图证明你的猜想．

    (6)用语言描述你证明的结果．

    查看答案和解析>>

    同步练习册答案