解:(1)由图象得
(300-100)÷20=10米/分;
设OA的解析式为y=kx,由题意,得
k=15,
故OA的解析式为:y=15x.
当x=2时,
y=15×2=30,
b=30米.
A(2,30).
(300-30)÷(10×3)=9,
则t=9+2=11.
则B(11,300)
故答案为:10,30,11.
(2)设AB的解析式为:y=k
1x+b
1,CD的解析式为y=k
2x+b
2,由题意,得
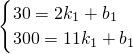
①或
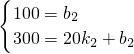
②,
解得:
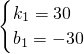
,

,
故线段AB的解析式为:y=30x-30,(2≤x≤11)
线段CD的解析式为:y=10x+100(0≤x≤20).
(3)由(2)得
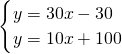
,
解得:

,
故登山6.5分钟时乙追上了甲.
分析:(1)由图象可以得出甲登山200米用的时间是20分钟就可以求出甲的速度,根据图象求出OA的解析式,当x=2时就可以求出y值,就是乙离地面的高度.用300-2分钟时的高度除以甲的速度的3倍就可以求出加速后用的时间,再加上2就是t的值.
(2)由(1)的结论,运用待定系数法就可以直接求出线段AB、CD的解析式.
(3)由(2)AB、CD的解析式建立二元一次方程组,求出方程组的解就求出了以追上甲的时间.
点评:本题是一道一次函数的综合试题,考查了行程问题中路程=速度×时间的关系变化的运用,待定系数法求一次函数的解析式的运用,图象的交点坐标的求法.在解答中注意线段的解析式要确定自变量的取值范围.

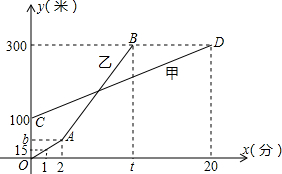 高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: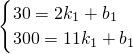 ①或
①或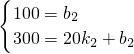 ②,
②,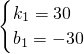 ,
, ,
,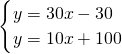 ,
, ,
,

 高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: