练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，∠ACB＝，AC＝BC，D为△ABC外一点，且AD＝BD，DE⊥AC交CA的延长线于E．求证：DE＝AE＋BC．

    答案：
    解析：

    　　证明：连结CD．

    　　∵AC＝BC且AD＝BD，

    　　∴C、D在AB的垂直平分线上，

    　　∴CD垂直平分AB，

    　　∴∠ACD＝∠ACB＝，(证明线段的和差关系问题，通常采用的方法是将不在同一直线上的线段转化为同一直线上的线段．)

    　　∵DE⊥CE，

    　　∴△CED为直角三角形，

    　　∴∠ACD＝∠EDC＝，

    　　∴CE＝DE．

    　　∵CE＝AE＋AC，AC＝BC，

    　　∴CE＝AE＋BC，

    　　∴DE＝AE＋BC．


    提示：

    注：此题要证明DE＝AE＋BC，需将AE、BC转化为同一直线上的线段，通过线段垂直平分线的性质，可以构造等腰直角三角形，证出∠ACD＝∠EDC＝，自然可以得到结论了．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：学习周报　数学　华师大八年级版　2009－2010学年　第10期　总第166期 华师大版 题型：044

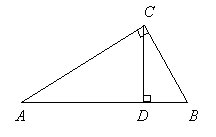
    某校把一块形状为直角三角形的废地开辟为植物园，如图所示，∠ACB＝90°，AC＝80米，BC＝60米，线段CD是一条水渠，且点D在边AB上．已知水渠的造价为10元/米，问当点D在距点A多远处时，水渠的造价最低？最低造价为多少？

    查看答案和解析>>

    科目：初中数学 来源：活学巧练八年级数学(下) 题型：044

    某校把一块形状为直角三角形的废地开辟为生物园，如图所示，∠ACB＝，AC＝80m，BC＝60m．

    (1)若入口E在边AB上，且与A、B等距离，求从入口E到出口C的最短路线长．

    (2)若线段CD是一条水渠，且D点在边AB上，已知水渠的造价为10元/平方米，问D点在距A点多远处时，此水渠的造价最低？最低造价是多少？

    查看答案和解析>>

    科目：初中数学 来源：1+1轻巧夺冠·优化训练·九年级数学下（北京课改版）·银版 题型：044

    某校把一块形状相似于直角三角形的地开辟为生物园，如图所示，∠ACB＝90°、BC＝60米、∠A＝36°．

    (1)若入口E在边AB上，且与A、B等距离，请你在图中画出入口E到C点的最短路线，并求出最短路线CE的长(保留整数)．

    (2)若线段CD是一条水渠，并且D点在边AB上，已知水渠造价为50元/米；水渠路线应如何设计才能使造价最低，请你画出水渠路线，并求出最低造价．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）在等腰Rt△ABC中，∠C＝90°，AC：BC：AB＝___________；

        （2）如图所示，∠ACB＝90°，∠A＝30°，则BC：AC：AB＝___________；若AB＝8，则AC＝___________；又若CD⊥AB，则CD＝___________。

        （3）等边△ABC的边长为a，则高AD＝___________，___________。

       

    查看答案和解析>>

    同步练习册答案