
 x+(2+
x+(2+ )分别交x轴,y轴于点A,C,点B为线段AC中点,连接OB,将△BOC折叠,使点B落在边OC上点F处,折痕为DE,EF∥x轴.
)分别交x轴,y轴于点A,C,点B为线段AC中点,连接OB,将△BOC折叠,使点B落在边OC上点F处,折痕为DE,EF∥x轴.
 ,0),求该抛物线的解析式;
,0),求该抛物线的解析式; S△GFP的点P?若存在,请求出点P横坐标的取值范围;若不存在,请说明理由.
S△GFP的点P?若存在,请求出点P横坐标的取值范围;若不存在,请说明理由. x+(2+
x+(2+ )=0,
)=0, -3,
-3, ,
, -3,0),C(0,2+
-3,0),C(0,2+ ),
), +3,OC=2+
+3,OC=2+ ,
,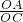 =
= =
= ,
, ),
), AC=2+
AC=2+ ,
, x,
x, x,
x, x=2+
x=2+ ,
, x=
x= ,2x=2,
,2x=2, ,1),F(0,1);
,1),F(0,1); ,
, ,
, x2-
x2- x+1;
x+1;
 x2-
x2- x+1=0,
x+1=0, ,x2=-2
,x2=-2 ,
, ,0),
,0), S△GFP,△GFP=△GFN+△GNP,
S△GFP,△GFP=△GFN+△GNP, x2-
x2- x+1=-2,
x+1=-2, x-18=0,
x-18=0, ,x2=-3
,x2=-3 ,
, ≤x<-2
≤x<-2 或
或 <x≤2
<x≤2 时,S△GFN≥
时,S△GFN≥ S△GFP.
S△GFP.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com