练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    规律探索：连接图（1）中的三角形三边的中点得图（2），再连接图；（2）中间的三角形三边的中点得图；（3），如此继续下去，那么在第n个图形中共有______个三角形．

    解：观察图形，发现：
    在第n个图形中共有1+4（n-1）=4n-3（个）．
    分析：观察图形，发现：在第（1）个是1个三角形的基础上，后边依次多4个三角形，推而广之，即可得到答案．
    点评：此类题要注意能够结合图形发现三角形的个数之间的规律，能够从特殊到一般，推而广之．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    16、规律探索：连接图（1）中的三角形三边的中点得图（2），再连接图；（2）中间的三角形三边的中点得图；（3），如此继续下去，那么在第n个图形中共有
    （4n-3）
    个三角形．

    查看答案和解析>>

    科目：初中数学 来源：2006年初中数学总复习下册 题型：059

    　　如图，某学习小组在探索“一点到等边三角形三边的距离与该等边三角形的高的关系”时，对话如下：

    　　甲同学：我们先将要探索的问题具体化，(边说边画)等边△ABC，高为h．点P该在哪儿呢？

    　　乙同学：我想，点P的位置就是分类讨论的关键．我们研究问题应该从特殊到一般．特殊的话，点P应该在等边△ABC的一边上，(边说边画，得图①)．只需连接AP，我就可以得到PD＋PE＝AM．

    　　丙同学：结果要及时上升为规律．设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3．你的发现就可以归纳为h＝h1＋h2＋h3．而点P在等边△ABC内部时(如图②)，这个结论也成立．

    　　丁同学：如果点P在等边△ABC外部呢(如图③)？丙发现的“规律”好像有问题……

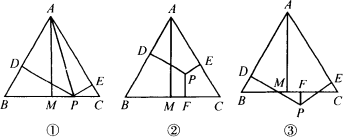
    (1)请你证明丙同学的发现．

    (2)丁同学发现了什么问题，提出你的猜想(不必证明)．

    查看答案和解析>>

    同步练习册答案