练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

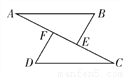
    如图所示,已知AB=DC,AB∥DC,AF=CE.求证:△ABE≌△CDF.

    证明见解析 【解析】试题分析：AB∥DC,则，又因AF=CE，所以AE=CF,已知AB=CD，由边角边可以得到△ABE≌△CDF. ∵AF=CE,∴AF+EF=CE+EF,∴AE=CF. ∵AB∥DC,∴∠EAB=∠FCD. 在△ABE和△CDF中, ∴△ABE≌△CDF.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    已知矩形的对角线与较长边所夹的角等于30°，那么较短边与两对角线所围成的三角形是________三角形．

    等边 【解析】如图，矩形ABCD中，对角线AC、BD交于点O，∠OBC=30°， ∵四边形ABCD是矩形，∴∠ABC=90°，OA=OB， ∵∠OBC=30°，∴∠ABO=∠ABC-∠OBC=60°， ∴△ABO是等边三角形， 故答案为：等边.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（1）练习 题型：解答题

    某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形．其中，抽屉底面周长为180cm，高为20cm．请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？（材质及其厚度等暂忽略不计）．

    当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3 【解析】【解析】 已知抽屉底面宽为x cm，则底面长为180÷2－x=（90－x）cm． 由题意得：。 ∴当x=45时，y有最大值，最大值为40500。 答：当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3。 根据题意列出二次函数关系式，然后利用二次函数的性质求最大值。 ...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）练习 题型：解答题

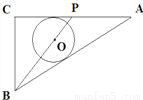
    如图，△ABC中，∠C＝90°，AC＝8cm，AB＝10cm，点P由点C出发以每秒2cm的速度沿CA向点A运动（不运动至A点），⊙O的圆心在BP上，且⊙O分别与AB、AC相切，当点P运动2秒钟时，求⊙O的半径.

    【解析】试题分析：设AC、AB与⊙O的切点分别为R、M，连接OR、OM，过O作OK⊥BC于K；由于△POR∽△PCB，可得出关于PR，OR，PC，BC的比例关系式，由此可求出PR与半径的比例关系．由此可表示出OK，AP的长；在Rt△OBK中，已知了OK的表达式，BK=BC-r，而OB可在Rt△OBM中用勾股定理求得．由此可根据勾股定理求出半径r的长． 试题解析： 连接OR、OM，如图所...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）练习 题型：单选题

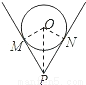
    一个钢管放在V形架内，如图是其截面图，O为钢管的圆心．如果钢管的半径为25cm，∠MPN=60°，则OP=（ ）

    A．50cm B．25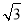cm C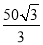．cm D．50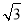cm

    A． 【解析】 试题分析：∵圆与V形架的两边相切， ∴△OMP是直角三角形中∠OPN=∠MPN=30°， ∴OP=2ON=50cm． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型：单选题

    下列条件中，能判定两个直角三角形全等的是( )

    A. 一锐角对应相等 B. 两锐角对应相等

    C. 一条边对应相等 D. 两条直角边对应相等

    D 【解析】试题分析：三角形全等可以利用SAS、SSS、ASA和AAS来进行判定，直角三角形还可以用HL定理来进行判定.本题中D选项可以利用SAS来进行判定三角形全等.

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册13.4课题学习 最短路径问题同步练习题 题型：解答题

    如图，牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD。若A到河岸CD的中点的距离为500米.

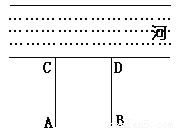
    （1）牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短? 用尺规作图在图中画出来

    （2）最短路程是多少?

    （1）作图见解析； （2）1000米． 【解析】 试题分析：作出点A关于河岸l的对称点A′，连接A′B，交河岸l于点D，则点D是牛饮水的位置．分析：根据轴对称的性质和“两点之间线段最短”，连接A′B，得到最短距离为A′B，再根据相似三角形的性质和A到河岸CD的中点的距离为500米，即可求出A'B的值． 试题解析：（1）作出A的对称点A′，连接A′B与CD相交于M，则牧童从A处把牛...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    已知A和B两点在线段EF的中垂线上，且∠EBF＝100°，∠EAF＝70°，则∠AEB等于( )

    A. 95° B. 15° C. 95°或15° D. 170°或30°

    C 【解析】因为A和B两点在线段EF的中垂线上，所以AE=AF，BE=BF， 所以∠AEF=∠AFE，∠BEF=∠BFE. 因为∠EBF＝100°，∠EAF＝70°， 所以∠AEF=(180°-70°)÷2=55°，∠BEF=(180°-100°)÷2=40°. ①当点A，B在EF的同侧时，∠AEB=∠AEF-∠BEF=55°-40°=15°； ②当点A，B在E...

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：解答题

    已知一次函数y=ax+b的图象经过点A(1,3)且与y=2x-3 平行．

    (1)求出a,b.写出y 与x 的函数关系；

    (2)求当x=-2 时，y的值，当y=10 时，x的值．

    (1)2 1 y=2x+1；（2）-1， . 【解析】试题分析：（1）根据两直线平行可得a的值，再将点A（1，3）代入即可得； （2）将x=-2，y=10分别代入解析式即可得. 试题解析：（1）∵一次函数 y ＝a x＋b的图象经过点 A(1，3)且与 y ＝2x－3 平行， ∴a=2， 把A (1，3)代入y=2x+b得，3=2×1+b，解得：b=1， ∴y与...

    查看答案和解析>>

    同步练习册答案