

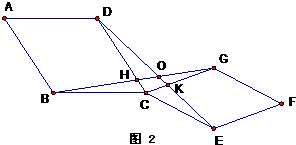
| 解:(1)线段AC,BD的数量关系是相等,直线AC,BD相交成90度角; | |
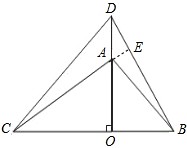
| (2)(1)中结论仍成立; 证明如下:如图延长CA交BD于点E, ∵等腰直角三角形OAB和OCD, ∴OA=OB,OC=OD, ∵AC2=AO2+CO2,BD2=OD2+OB2, ∴AC=BD; ∴△DOB≌△COA(SSS), ∴∠CAO=∠DBO,∠ACO=∠BDO, ∵∠ACO+∠CAO=90°, ∴∠ACO+∠DBO=90°,则∠AEB=90°, 即直线AC,BD相交成90°角。 |
 |
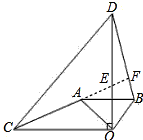
| (3)结论仍成立;如图延长CA交OD于E,交BD于F, ∵∠COD=∠AOB=90°, ∴∠COA+∠AOD=∠AOD+∠DOB,即:∠COA=∠DOB, ∵CO=OD,OA=OB, ∴△COA≌△DOB(SAS), ∴AC=BD,∠ACO=∠ODB; ∵∠CEO=∠DEF, ∴∠COE=∠EFD=90°, ∴AC⊥BD,即直线AC,BD相交成90°角。 |
 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届江苏省初三第一学期期中考试数学试卷 题型:解答题
如图甲,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
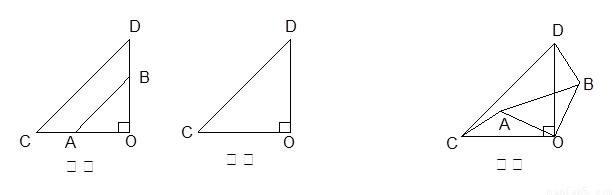
1.在图甲中,你发现线段AC、BD的数量关系是_______,直线AC、BD相交成____度角
2.将图甲中的 绕点O顺时针旋转
绕点O顺时针旋转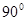 ,在图乙中作出旋转后的
,在图乙中作出旋转后的 ;
;
3.将图甲中的 绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若
绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若 绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com