
 .
.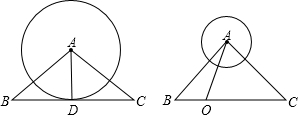
 ,
, =2,
=2,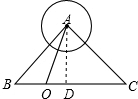
 =2,
=2, ,
,
 ,
, -
- )2+(
)2+( )2,
)2,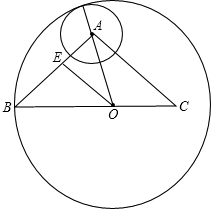
 ,
, ;
; -
- )2+(
)2+( )2,
)2, ,
, =
= ,
, 或
或 .
. ,根据勾股定理即可推出BD=4,即可推出AD=BD=CD=2;
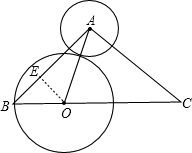
,根据勾股定理即可推出BD=4,即可推出AD=BD=CD=2; ,在△AEO中 AO2=AE2+OE2=(AB-BE)2+OE2,推出(1+x)2=(2
,在△AEO中 AO2=AE2+OE2=(AB-BE)2+OE2,推出(1+x)2=(2 -
- )2+(
)2+( )2,求出x=
)2,求出x= ,由①的结论可知△AOC面积=y=4-x,即可推出△AOC的面积;当两圆内切时,OA=x-1,然后把OA代入到 AO2=AE2+OE2=(AB-BE)2+OE2,即可推出x的值,即可推出△AOC面积.
,由①的结论可知△AOC面积=y=4-x,即可推出△AOC的面积;当两圆内切时,OA=x-1,然后把OA代入到 AO2=AE2+OE2=(AB-BE)2+OE2,即可推出x的值,即可推出△AOC面积.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| S△BPQ |
| S△ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
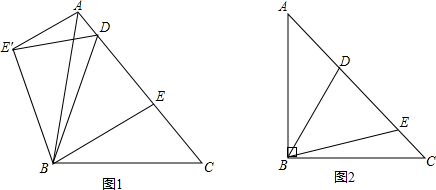
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com