练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    x－10＝5可变形为x＝5＋________．

    答案：10
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    (10分)

    问题提出
    我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式M、N的大小，只要作出它们的差M－N，若M－N＞0，则M＞N；若M－N＝0，则M＝N；若M－N＜0，则M＜N．
    问题解决
    如图1，把边长为a＋b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．

    解：由图可知：M＝a2＋b2，N＝2ab．
    ∴M－N＝a2＋b2－2ab＝(a－b)2．
    ∵a≠b，∴(a－b)2＞0．
    ∴M－N＞0．
    ∴M＞N．
    类别应用
    (1)已知小丽和小颖购买同一种商品的平均价格分别为元/千克和元/千克(a、b是正数，且a≠b)，试比较小丽和小颖所购买商品的平均价格的高低．
    (2)试比较图2和图3中两个矩形周长M1、N1的大小(b＞c)．
    联系拓广
    小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图4所示(其中b＞a＞c＞0)，售货员分别可按图5、图6、图7三种方法进行捆绑，吻哪种方法用绳最短？哪种方法用绳最长？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（山东青岛卷）数学（解析版） 题型：解答题

    在前面的学习中，我们通过对同一面积的不同表达和比较，根据图①和图②发现并验证了平方差公式和完全平方公式

    这种利用面积关系解决问题的方法，使抽象的数量关系因集合直观而形象化。

    【研究速算】

    提出问题：47×43，56×54，79×71，……是一些十位数字相同，且个位数字之和是10的两个两位数相乘的算式，是否可以找到一种速算方法？

    几何建模：

    用矩形的面积表示两个正数的乘积，以47×43为例：

    （1）画长为47，宽为43的矩形，如图③，将这个47×43的矩形从右边切下长40，宽3的一条，拼接到原矩形的上面。

    （2）分析：原矩形面积可以有两种不同的表达方式，47×43的矩形面积或（40＋7＋3）×40的矩形与右上角3×7的矩形面积之和，即47×43＝（40＋10）×40＋3×7＝5×4×100＋3×7＝2021，用文字表述47×43的速算方法是：十位数字4加1的和与4相乘，再乘以100，加上个位数字3与7的积，构成运算结果。

    归纳提炼：

    两个十位数字相同，并且个位数字之和是10的两位数相乘的速算方法是（用文字表述）        .

    【研究方程】

    提出问题：怎么图解一元二次方程

    几何建模：

    （1）变形：

    （2）画四个长为，宽为的矩形，构造图④

    （3）分析：图中的大正方形面积可以有两种不同的表达方式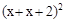，或四个长，宽的矩形之和，加上中间边长为2的小正方形面积

    即：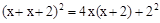

    ∵

    ∴

    ∴

    ∵

    ∴

    归纳提炼：求关于的一元二次方程的解

    要求参照上述研究方法，画出示意图，并写出几何建模步骤（用钢笔或圆珠笔画图，并标注相关线段的长）

    【研究不等关系】

    提出问题：怎么运用矩形面积表示与的大小关系（其中）？

    几何建模：

    （1）画长，宽的矩形，按图⑤方式分割

    （2）变形：

    （3）分析：图⑤中大矩形的面积可以表示为；阴影部分面积可以表示为，

    画点部分的面积可表示为，由图形的部分与整体的关系可知：＞，即

    ＞

    归纳提炼：

    当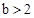，时，表示与的大小关系

    根据题意，设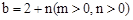，，要求参照上述研究方法，画出示意图，并写出几何建模步骤（用钢笔或圆珠笔画图，并标注相关线段的长）

     

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江杭州萧山高桥初中九年级上学期期初摸底考试数学试卷（解析版） 题型：选择题

    一元二次方程x2－4x－6＝0，经过配方可变形为（　　）

    A.(x－2)2＝10       B.(x－2)2＝6    C.(x－4)2＝6    D.(x－2)2＝2

     

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（湖北黄石卷）数学 题型：解答题

    (10分)

    问题提出

    我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式M、N的大小，只要作出它们的差M－N，若M－N＞0，则M＞N；若M－N＝0，则M＝N；若M－N＜0，则M＜N．

    问题解决

    如图1，把边长为a＋b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．

    解：由图可知：M＝a2＋b2，N＝2ab．

    ∴M－N＝a2＋b2－2ab＝(a－b)2．

    ∵a≠b，∴(a－b)2＞0．

    ∴M－N＞0．

    ∴M＞N．

    类别应用

    (1)已知小丽和小颖购买同一种商品的平均价格分别为元/千克和元/千克(a、b是正数，且a≠b)，试比较小丽和小颖所购买商品的平均价格的高低．

     (2)试比较图2和图3中两个矩形周长M1、N1的大小(b＞c)．

     

     

     

     

     

     

     

    联系拓广

    小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图4所示(其中b＞a＞c＞0)，售货员分别可按图5、图6、图7三种方法进行捆绑，吻哪种方法用绳最短？哪种方法用绳最长？请说明理由．

    查看答案和解析>>

    同步练习册答案