
 已知△ABC的内切圆半径为r,∠A=60°,
已知△ABC的内切圆半径为r,∠A=60°,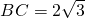 ,则r的取值范围是________.
,则r的取值范围是________.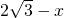 .运用∠A=60°用内切圆半径表示AE的长,进而通过x、r表示出AC、AB的长,并表示出△ABC的面积.再将△ABC的面积用三个小三角形面积的和表示出来.这样就建立起了关于x、r的关系式.将关系式看做关于x的一元二次方程判定r的取值范围.结合实际r的最后取值范围即可确定.
.运用∠A=60°用内切圆半径表示AE的长,进而通过x、r表示出AC、AB的长,并表示出△ABC的面积.再将△ABC的面积用三个小三角形面积的和表示出来.这样就建立起了关于x、r的关系式.将关系式看做关于x的一元二次方程判定r的取值范围.结合实际r的最后取值范围即可确定.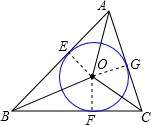 解:方法1:设CF的长为x,则BF的长为
解:方法1:设CF的长为x,则BF的长为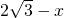 .
.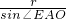 =
=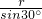 =2r,AE=AO•cos30°=
=2r,AE=AO•cos30°=
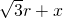 ,AB=AE+BE=
,AB=AE+BE=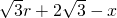
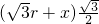
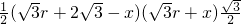
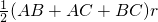 =
=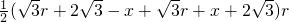
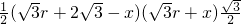 =
=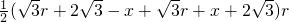
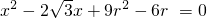
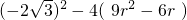 ≥0,即3r2-2r-1≤0
≥0,即3r2-2r-1≤0
 AB•AC•sinA=
AB•AC•sinA= (a+b+c)r
(a+b+c)r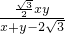 ①
① r=
r= (x+y-2
(x+y-2 )
) (r+1)xy=2
(r+1)xy=2 y(r+1)-y 2
y(r+1)-y 2 y2-3(r+1)y+(2
y2-3(r+1)y+(2 r2+4
r2+4 r)=0
r)=0

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2012年沪科版初中数学九年级下26.6三角形的内切圆练习卷(解析版) 题型:解答题
如图,已知△ABC的内切圆⊙O分别和边BC,AC,AB切于D,E,F,如果AF=2,BD=7,CE=4.
(1)求△ABC的三边长;
(2)如果P为 上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.
上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com